正则集、正则式,右线性文法,正则表达式与有限自动机之间的图示关系,右线性语言与有限自动机之间的关系。
正则集和正则式
- 正则集可用正则式表示。字母表 T 上的一个正则式和它表示的正则集可递归定义如下:
- ε 和 ∅ 都是正则式,分别表示的正则集是 {ε} 和空集 ∅;
- 任意 a ∈ T 是正则式,他表示的正则集是 {a}(以上两条为原子正则式);
- 如果 A 和 B 是正则式,分别表示的正则集是 L(A) 和 L(B),则 (A+B)、(A·B)、(A) 也都是正则式,分别表示的正则集是
L(A) ∪ L(B)、L(A)L(B)、`L(A)。操作的优先级为*(闭包) > ·(连接)> +(联合)`。
- 仅由 有限次 使用以上三步定义的表达式才是字母表 T 的正则式。如果两个正则式表示相同的正则集,则称两个正则式相等。
- 假设 α、β、γ 都是正则式,则:
(α + β) + γ = α + (β + γ)(α · β) · γ = α · (β · γ)α + β = β + αα + α = αα · (β + γ) = (α · β) + (α · γ)(β + γ) · α = (β · α) + (γ · α)α + ∅= α(零元)α · ∅ = ∅ · α = ∅(零元)α · ε = ε · a = a(幺元)(α*)* = α*(闭包)α* = ε + α+∅* = ε
- 注意:
- 正则集是 T* 的子集;
- L+ 包含 ε 当且仅当 L 包含 ε;
- 每个正则集至少对应一个正则式。
右线性文法与正则
右线性文法与正则式
- 右线性文法(正则文法)与正则式具有等价性。
- 求解规则:设
x = αx + β, α ∈ T*, β ∈ (N∪T)*, x ∈ N,可解出x = α*β。 - 例:
G = {N = {S, A, B}, T = {a, b}, P, S},其中 P 包括以下规则:S → aA, S → bB, S → b, A → bA, A → ε, B → bS。- 将 P 中的推导式联立,可得到
S = aA + bB + b,A =bA + ε和B = bS; - 根据
A = bA + ε,应用求解规则得到A = b*; - 将
A = b*,B = bS代入,得到S = ab* + bbS + b,转换形式得到S = (bb)S + (ab* + b); - 在此应用求解规则得到
S = (bb)*(ab*+b)。
- 将 P 中的推导式联立,可得到
右线性文法与正则集
- 正则集是由右线性文法产生的语言,二者是等同的 ,按照上面定义的正则集都是右线性文法产生的语言。
- 设字母表为 T。∅、{ε} 和 {a}(任意 a ∈ T)都是正则集,则 ∅、{ε} 和 {a} 都是右线性语言。它们分别对应的右线性文法是
G∅ = ({S}, T, ∅, S)、G{ε} = ({S}, T, {S → ε}, S)以及G{a} = ({S}, {a}, {S → a}, S)。 - 可证明,设字母表 T 上有右线性语言 L1 和 L2,则 L1∪L2、L1L2 和 L1* 都是右线性语言。
- 证 L1 ∪ L2 为右线性语言:有右线性文法
G = (N, T, P, S),其中N = N1 ∪ N2 ∪ {S},P = P1 ∪ P2 ∪ {S → S1, S → S2},S ∉ N1 ∪ N2,是一个新的非终结符; - 证 L1L2 为右线性语言:有右线性文法
G = (N, T, P, S),其中 N = N1 ∪ N2,S = S1,生成式 P 为:若 A → αB ∈ P1 则 A → αB ∈ P,若 A → α ∈ P1,则 A → αS2 ∈ P,P2 ⊆ P。 - 证 L1* 是右线性语言:有右线性文法
G = (N, T, P, S),其中 N = N1 ∪ {S},S ∉ N1,S 是一个新非终结符,生成式 P 定义为:若 A → αB ∈ P1 则 A → αB ∈ P,若 A → α ∈ P1 则 A → αS ∈ P 且 A → α ∈ P,且 P 中包括 {S → S1, S → ε}。
- 证 L1 ∪ L2 为右线性语言:有右线性文法
正则表达式和有限自动机
以下图片均来自王柏教授(北京邮电大学大数据科学与服务中心)的《形式语言与自动机》课件。
- 有限自动机、右(左)线性文法和正则表达式都定义了同一种语言(正则语言)。
- 由 DFA 构造等价的正则表达式(状态消去法):
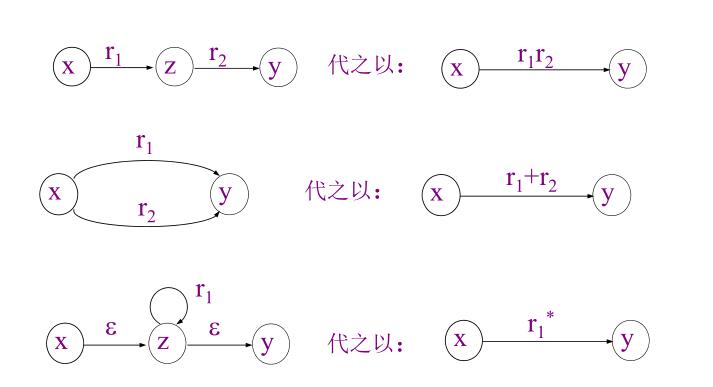
- 从 DFA 构造等价正则表达式的具体步骤如下:
- 对每一终态 q,依次消去除 q 和初态 q0 之外的其它状态;
- 若 q ≠ q0,最终可得到一般形式:
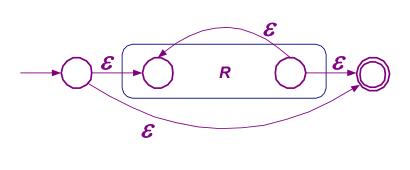
(R+ SU*T)*SU*,如下图中左侧的自动机; - 若 q = q0,最终可得到如图中右侧的自动机,对应正则式为
R*; - 最终的正则表达式为 每一终态对应的正则表达式之和(联合) 。

- 从正则表达式构建等价的 ε-NFA,可根据如下几种基本组合子组合:
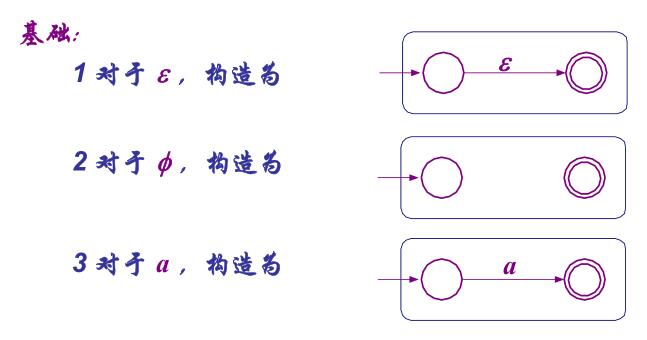
- 对于
R+S、RS以及R*,分别为下图中从上到下三种连接方式: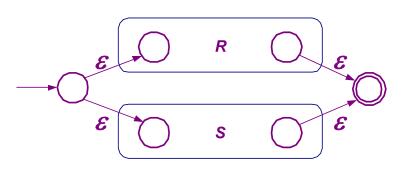
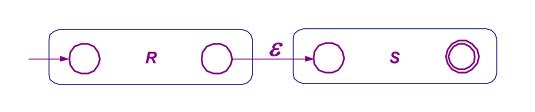
右线性文法与有限自动机
右线性文法 ⇒ 有限自动机
- 设右线性文法 G = (N, T, P, S),产生语言为 L(G),则存在一个有限自动机 M 接受语言 L(M) = L(G)。
- 构造:构造一个与 G 等价的 NFA M = (Q, T, δ, q0, F),其中
- Q = N ∪ {H},H 为新增状态,H ∉ N;
- q0 = S;
- 当 S → ε ∈ P 时,F = {H, S},否则 F = {H};
- δ 的定义为:若 A → αB ∈ P 则 B ∈ δ(A, α),若 A → α ∈ P 则 H ∈ δ(A, α),且对任意输入有 δ(H, α) = ∅。
- 例:G = ({S, B}, {α, β}, P, S),其中 P 为 S → αB, B → αB | βS | α。
- 令 NFA M = (Q, T, δ, q0, F),Q = {S, B, H},T = {α, β},q0 = S,F = {H};
- ∵ S → αB,故 δ(S, α) 中包括 B;
- ∵ B → αB,故 δ(B, α) 中包括 B;
- ∵ B → βS,故 δ(B, β) 中包括 S;
- ∵ B → α,故 δ(B, α) 中包括 H。
有限自动机 ⇒ 右线性文法
- 设 DFA M 接受的语言为 L(M),则存在右线性文法 G,它产生的语言 L(G) = L(M)。
- 构造:设 M = (Q, T, δ, q0, F),则令 G = (N, T, P, S),其中
- N = Q,S = q0;
- 若 δ(A, α) = B 且 B ∉ F 则 A → αB ∈ P;
- 若 δ(A, α) = B 且 B ∈ F 则 A → α ∈ P,A → αB ∈ P。
- 对于 NFA,可以转换为等价的 DFA 再做相应构造。
右线性语言性质
TODO
专栏目录:计算机理论基础
此专栏的上一篇文章:有限自动机
此专栏的下一篇文章:暂无
参考资料:《形式语言与自动机》,王柏、杨娟编著,北京邮电大学出版社
原创作品,允许转载,转载时无需告知,但请务必以超链接形式标明文章原始出处(http://blog.forec.cn/2017/03/19/formal-languages-and-automata3/) 、作者信息(Forec)和本声明。