第8章的线性回归创建的模型需要拟合所有的样本点(除了局部加权线性回归)。当数据拥有众多特征并且特征之间关系十分复杂时,构建全局模型的想法就比较困难,并且生活中很多问题是非线性的,无法用全局线性模型来拟合所有数据。一种方法是将数据集递归地切分成很多份易建模的数据,并对可以拟合的小数据集用线性回归建模。
复杂数据的局部性建模
- 在Chapter03中介绍了贪心算法的决策树,构建算法是ID3,每次选取当前最佳特征来分割数据,并且按照这个特征的所有可能取值来划分,一旦切分完成,这个特征在之后的执行过程中不会再有任何用处。这种方法切分过于迅速,并且需要将连续型数据离散化后才能处理,这样就破坏了连续变量的内在性质。
- 二元切分法是另一种树构建算法,每次将数据集切分成两半,如果数据的某个特征满足这个切分的条件,就将这些数据放入左子树,否则右子树。二元切分法也节省了树的构建时间,但树一般都是离线构建,因此意义不大。CART(Classification And Regression Trees,分类回归树)使用二元切分来处理连续型变量,并用
R^2取代香农熵来分析模型的效果。
连续和离散型特征的树的构建
使用字典存储树的数据结构,每个节点包含以下四个元素:待切分的特征、待切分的特征值、左子树、右子树。Chapter03中的每个节点可能有多个孩子,因此使用字典存储,而CART可以固定数据结构,因为每个非叶节点固定包含两个子树。下面创建回归树(叶节点包含单个值)和模型树(叶节点存储一个线性方程),创建树的代码可以重用,伪代码大致如下。
- 找到最佳的待切分特征:
- 如果该节点不能再分,将该节点存为叶节点
- 执行二元切分
- 在左右子树分别递归调用
CART算法实现 - regTrees.py。binSplitDataSet通过数组过滤切分数据集,createTree递归建立树,输入参数决定树的类型,leafType给出建立叶节点的函数,因此该参数也决定了要建立的是模型树还是回归树,errType代表误差计算函数,ops是一个包含树构建所需的其他参数的元组。代码中的chooseBestSplit函数选取最佳分类方式,尚未实现。github上的附书源码有错误,binSplitDataSet的两行最后没有
[0]。
1 | from numpy import * |
将CART算法用于回归
- 如何实现数据切分要取决于叶节点的建模方式,回归树假设叶节点是常数值,可以通过计算数据的总方差代替香农熵判断数据的混乱度。
函数chooseBestSplit的目标是找到数据切分的最佳位置,它遍历所有的特征及其可能的取值来找到使误差最小化的划分阈值。伪代码大致如下。
- 对每个特征:对每个特征值:
- 将数据集划分为两份
- 计算切分的误差
- 若当前误差小于最小误差,则更新
- 返回最佳切分特征和阈值
回归树切分函数 - regTrees.py,regLeaf负责生成叶节点,在回归树中,该模型是目标变量的均值。regErr是误差估计函数,计算目标变量总方差。chooseBestSplit的参数中为ops设定了tolS和tolN,tolS是容许的误差下降值,tolN是切分的最小样本数。在三种情况下chooseBestSplit会停止切分:误差下降不够大、切分子集数目小、剩余的特征值都相同。github的附书源码也有问题,chooseBestSplit函数中,
for splitVal in set(dataSet[:,featIndex]):要增加.T.tolist()[0]否则会报无法hash的错误。
1 | def regLeaf(dataSet): |
- 测试代码效果,数据来自ex00.txt和ex0.txt,用matplotlib绘制的图像如下。
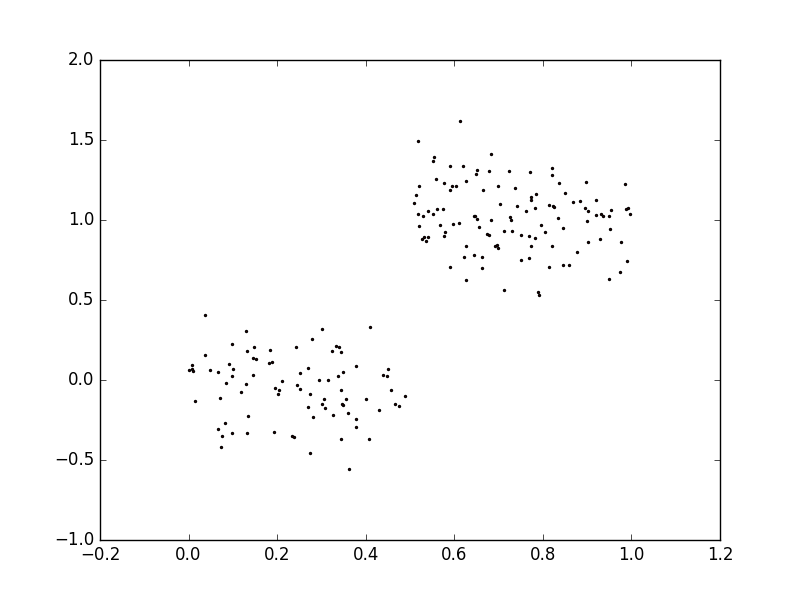
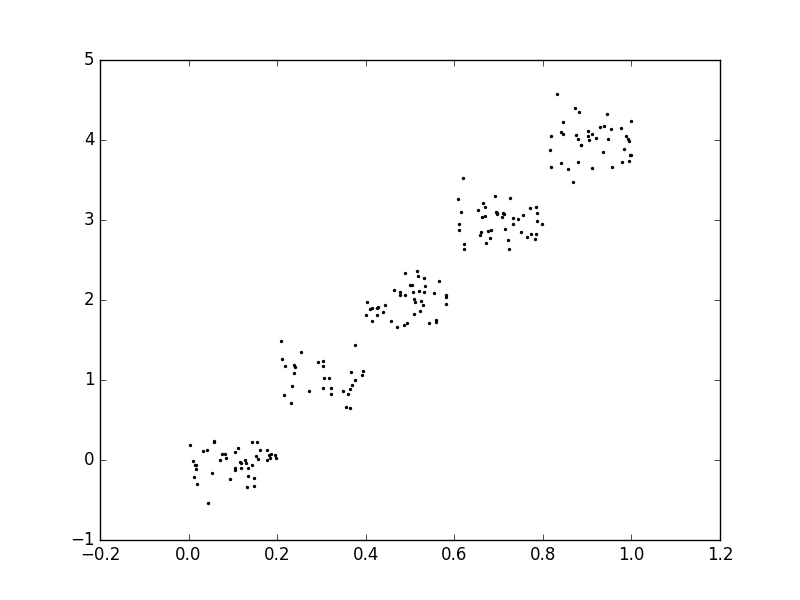
1 | >>> reload(regTrees) |
树剪枝
如果树节点过多,则该模型可能对数据过拟合,通过降低决策树的复杂度来避免过拟合的过程称为剪枝。在函数chooseBestSplit中的三个提前终止条件是“预剪枝”操作,另一种形式的剪枝需要使用测试集和训练集,称作“后剪枝”。
预剪枝
- 树构建算法对输入的tolS和tolN非常敏感,将ops换为(0,1)会发现生成的树非常臃肿,几乎为数据集中的每个样本都分配了一个叶节点。加载ex2.txt的数据,该数据集和前面ex00.txt的数据分布类似,但数量级是后者的100倍,在这种情况下,ex00构建出的树只有两个叶节点,而ex2构建出的树有非常多的叶节点。原因在于停止条件tolS对误差的数量级非常敏感。显然,通过不断修改停止条件并且比较哪个条件更好并不合理,多数情况下我们并不确定要寻找什么样的结果,计算机应该给出总体的概貌。
后剪枝
- 使用后剪枝方法需要将数据集交叉验证,首先给定参数,使得构建出的树足够复杂,之后从上而下找到叶节点,判断合并两个叶节点是否能够取得更好的测试误差,如果是就合并。下面是回归树剪枝函数。函数isTree测试输入变量是否为一棵树,getMean对树进行塌陷处理,计算整棵树的平均值。prune函数对树剪枝,参数tree为待剪枝的树,testData是测试集。需要注意的是,测试集合训练集样本的取值范围不一定相同。
1 | def isTree(obj): |
模型树
- 将叶节点设置为分段线性函数,分段线性指模型由多个线性片段组成。例如下图的数据,可以由0.0~0.3和0.3~1.0的两条直线组成。决策树相比其他机器学习算法易于理解,而模型树的可解释性是它优于回归树的特性之一。模型树同时具备更高的预测准确度。
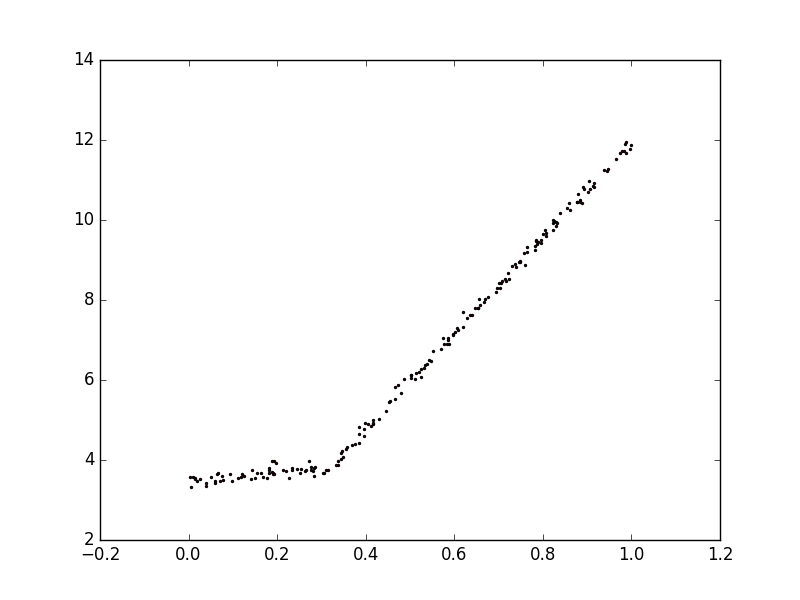
- 前面的代码已经给出了构建树的代码,只要修改参数errType和leafType。对于给定的数据集,先用现行的模型对它进行拟合,然后计算真实目标值和模型预测值之间的差距。最后求这些差值的平方和作为误差。modelLeaf函数生成叶节点,linearSolve返回回归系数,modelErr在数据集上调用linearSove,返回yHat和y之间的平方误差。
1 | def linearSolve(dataSet): |
树回归和标准回归的比较
- 对于输入的单个数据点,函数treeForeCast返回一个预测值。参数modelEval是对叶节点数据进行预测的函数的引用,函数treeForeCast自顶向下遍历整棵树,直到命中叶节点为止。一旦到达叶节点,它会在输入数据上调用modelEval,该参数默认值是regTreeEval。要对回归树叶节点预测,就调用regTreeEval,要对模型树节点预测,调用modelTreeEval。
1 | def regTreeEval(model, inDat): |
- 比较回归树、模型树和标准线性回归的
R^2数值。可以看出,模型树的结果比回归树好,而树回归方法在预测复杂数据时会比简单的线性模型更有效。
1 | >>> trainMat = mat(regTrees.loadDataSet('bikeSpeedVsIq_train.txt')) |
Tkinter库创建GUI
- Tkinter模块的.grid()方法将widget安排在一个二维表格内,,默认widget会显示在0行0列,可以通过设定columnspan和rowspan来告诉布局管理器是否允许一个widget跨行或跨列。界面代码如下 - treeExplore.py。
1 | from numpy import * |
- Matplotlib的构建程序包含一个前端面向用户,如plot和scatter方法等,同时创建一个后端,用于实现绘图和不同应用程序之间的接口。改变后端可以将图像绘制不同格式的文件上,将后端在设置为TkAgg,可以在所选GUI框架上调用Agg,呈现在画布上。下面的代码填补了上面的两个占位函数,另外将上面代码中加载文件的语句移入了按钮事件。
1 | import matplotlib |
- 绘制出的GUI界面如下。
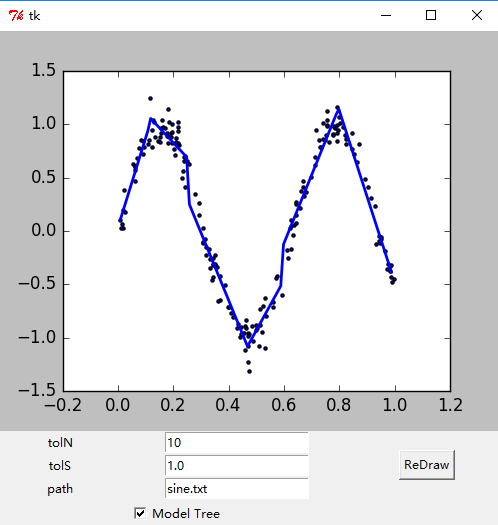
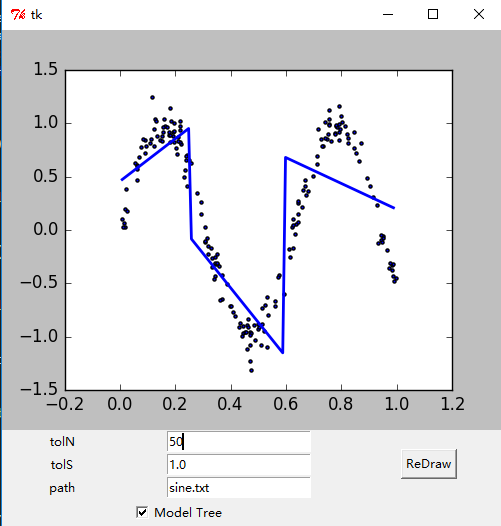
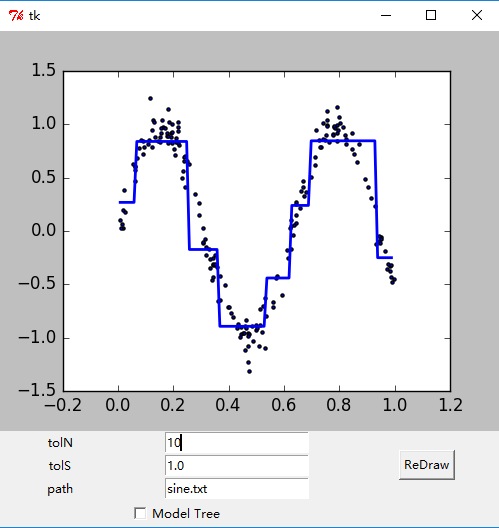
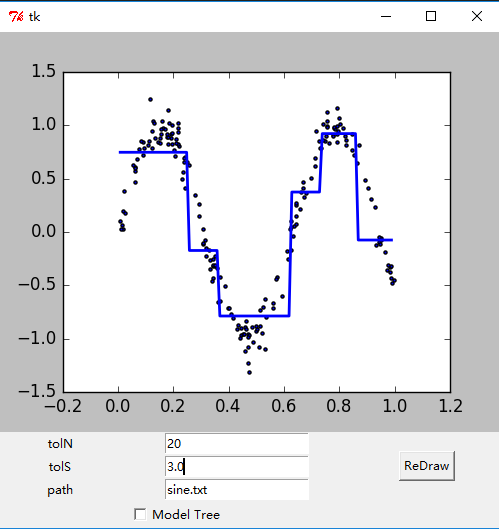
参考文献: 《机器学习实战 - 美Peter Harrington》
原创作品,允许转载,转载时无需告知,但请务必以超链接形式标明文章原始出处(https://forec.github.io/2016/02/20/machinelearning9/) 、作者信息(Forec)和本声明。