机器学习笔记（Chapter 08 - 回归）

回归是前面监督学习方法的延续，监督学习指的是有目标变量或者预测目标的机器学习方法。回归于分类的不同在于其目标变量是连续数值型。

线性回归找到最佳拟合曲线

• 线性回归结果易于理解，计算上不复杂，但对非线性的数据拟合不好。适用于数值型和标称型数据。
• 回归的目的是预测数值型的目标值。最直接的办法是根据输入写出一个目标值的计算公式，这个公式就是回归方程。求解回归系数的过程就是回归。回归一般指线性回归，本章中二者同义。线性回归意味着可以将输入项分别乘以一些常量，再将结果加起来得到输出，而非线性回归模型则认为输出可能是输入的乘积。
• 回归的一般方法
  • 收集数据：任意方法
  • 准备数据：需要数值型数据，标称型数据将被转换成二值型数据。
  • 分析数据：绘出数据的可视化二维图有助于对数据做出理解和分析。在采用所见发求得新回归系数后，可以将新拟合线在图上作为对比。
  • 训练算法：找到回归系数。
  • 测试算法：使用R^2或者预测值和数据的拟合度来分析模型的效果。
  • 使用算法：使用回归可以在给定一个输入的时候预测一个数值，这是对分类方法的提升，可以预测连续性数据而不仅仅是离散的类别标签。
• 求解回归系数：假定输入数据存放在矩阵X中，回归系数存放在向量W中，对于给定的数据X1，预测结果会通过Y1=X^T·W给出。要找到W，最常用的方法是找出使误差最小的W。误差指预测y值和真实y值之间的差值，使用该误差的简单累加会使正负误差相互抵消，因此采用平方误差。平方误差写作∑(y'-x^T·W)^2，用矩阵表示写作(y-Xw)^T·(y-Xw)，如果对w求导，就得到X^T·(Y-Xw)，令其为零，解出w=(X^T·X)^(-1)·X^T·y。注意公式中包含了(X^T·X)^(-1)，因此要在代码中判断矩阵是否可逆。该方法称为OLS（普通最小二乘法）。

• 下面是原始数据点的分布

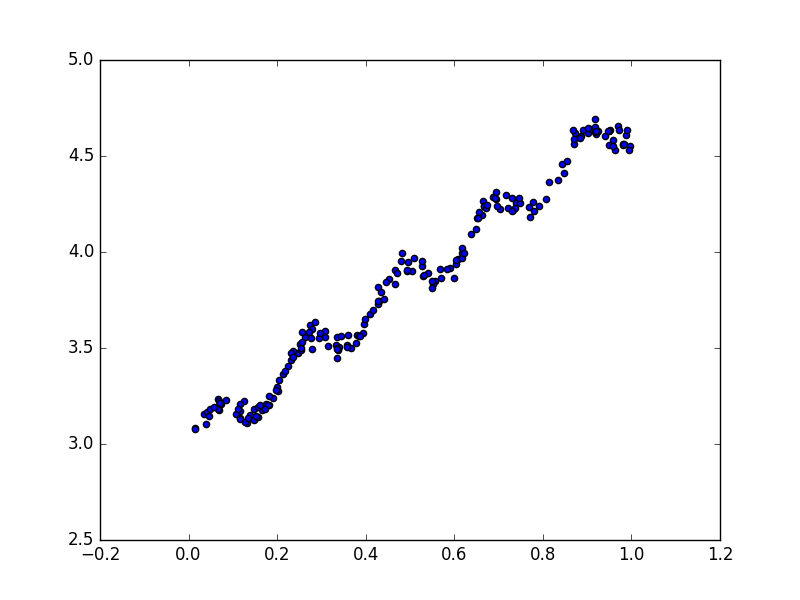
• 标准回归函数和数据导入函数 - regression.py

from numpy import *

def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t')) - 1
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

def standRegres(xArr, yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T * xMat
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do reverse"
        return
    ws = xTx.I * (xMat.T * yMat)
    return ws

• 生成的线性回归效果图如下

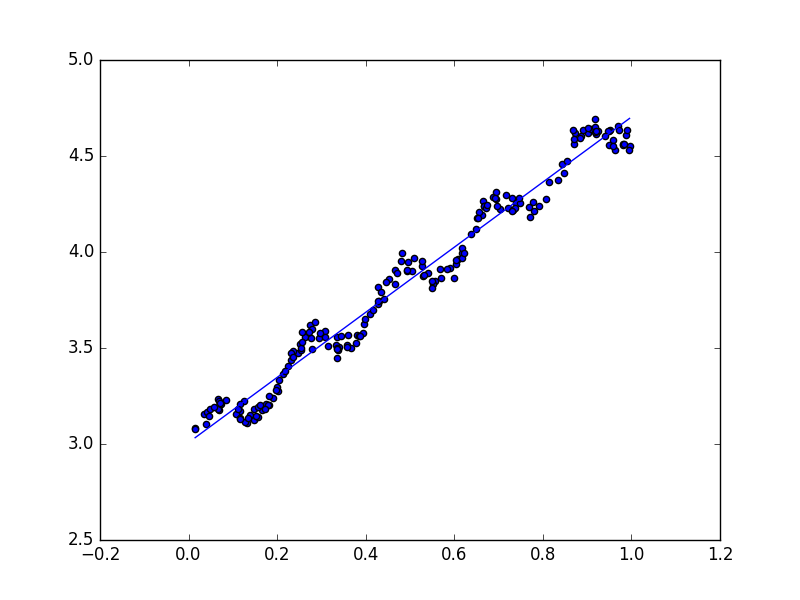
• Numpy库提供了corrcoef(yEstimate, yActure)方法来计算预测值和真实值的相关性。下面的交互代码结果中，yMat和自己匹配是最完美的，而yHat和yMat的相关系数为0.98。

>>> yHat = xMat * ws
>>> corrcoef(yHat.T, yMat)
array([[1.        , 0.98647356],
       [0.98647356, 1.        ]])

局部加权线性回归 LWLR

• 最佳拟合直线方法将数据视为直线建模，但数据似乎有其他潜在模式。线性回归的一个问题是有可能出现欠拟合现象，因为他求的是具有最小均方误差的无偏估计。因此有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。其中一个方法是局部加权线性回归（Locally Weighted Linear Regression）。在该算法中，为待测点附近的每个点赋予一定的权重，然后在这个子集上基于最小均方差来进行普通的回归。和kNN一样，这种算法每次预测都需要先选取出对应的数据子集。解出回归系数w的形式如下w=(X^T·WX)^(-1)·X^T·W·y，其中W是一个矩阵，用来给每个数据点赋予权重。

• LWLR使用“核”（和SVM类似）来为附近的点赋予更高的权重。类似kNN，LWLR认为样本点距离越近，越有可能符合同一个线性模型。高斯核对应权重如下w(i,i) = exp(|x'-x|/(-2k^2))。这样就构建了只含对角元素的权重矩阵W，并且点x和x(i)越近，w(i,i)就越大。参数k由用户指定，决定了对附近的点赋予多大的权重。当k较大时，更多的数据被用来训练回归模型，当k较小时，仅有很少的局部点被用来训练回归模型。

• 局部加权线性回归函数 - regression.py

def lwlr(testPoint, xArr, yArr, k = 1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye(m))
    for j in range(m):
        diffMat = testPoint - xMat[j,:]
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do reverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

def lwlrTest(testArr, xArr, yArr, k = 1.0):
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat

• 添加代码绘制在不同k的情况下局部加权线性回归结果的拟合情况。

def drawPlotAboutK():
    xArr, yArr = loadDataSet('ex0.txt')
    xMat = mat(xArr)
    srtInd = xMat[:,1].argsort(0)
    xSrot = xMat[srtInd][:,0,:]
    import matplotlib.pyplot as plt
    fig = plt.figure()
    ax = fig.add_subplot(211)
    yHat01 = lwlrTest(xArr, xArr, yArr, 0.01)
    ax.plot(xSrot[:,1],yHat01[srtInd])
    ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0], s =2, c='green')
    ax = fig.add_subplot(212)
    yHat001 = lwlrTest(xArr, xArr, yArr, 0.003)
    ax.plot(xSrot[:,1],yHat001[srtInd])
    ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0], s =2, c='green')
    plt.show()

• 上面代码绘制出结果如下，可以看出当k=0.003时纳入了太多的噪声点，k=1时的结果和使用最小二乘法的标准线性回归类似，k=0.01时的模型效果最好，平滑并且挖掘出数据内在规律。上图是k=0.01的情况，下图是k=0.003的情况。
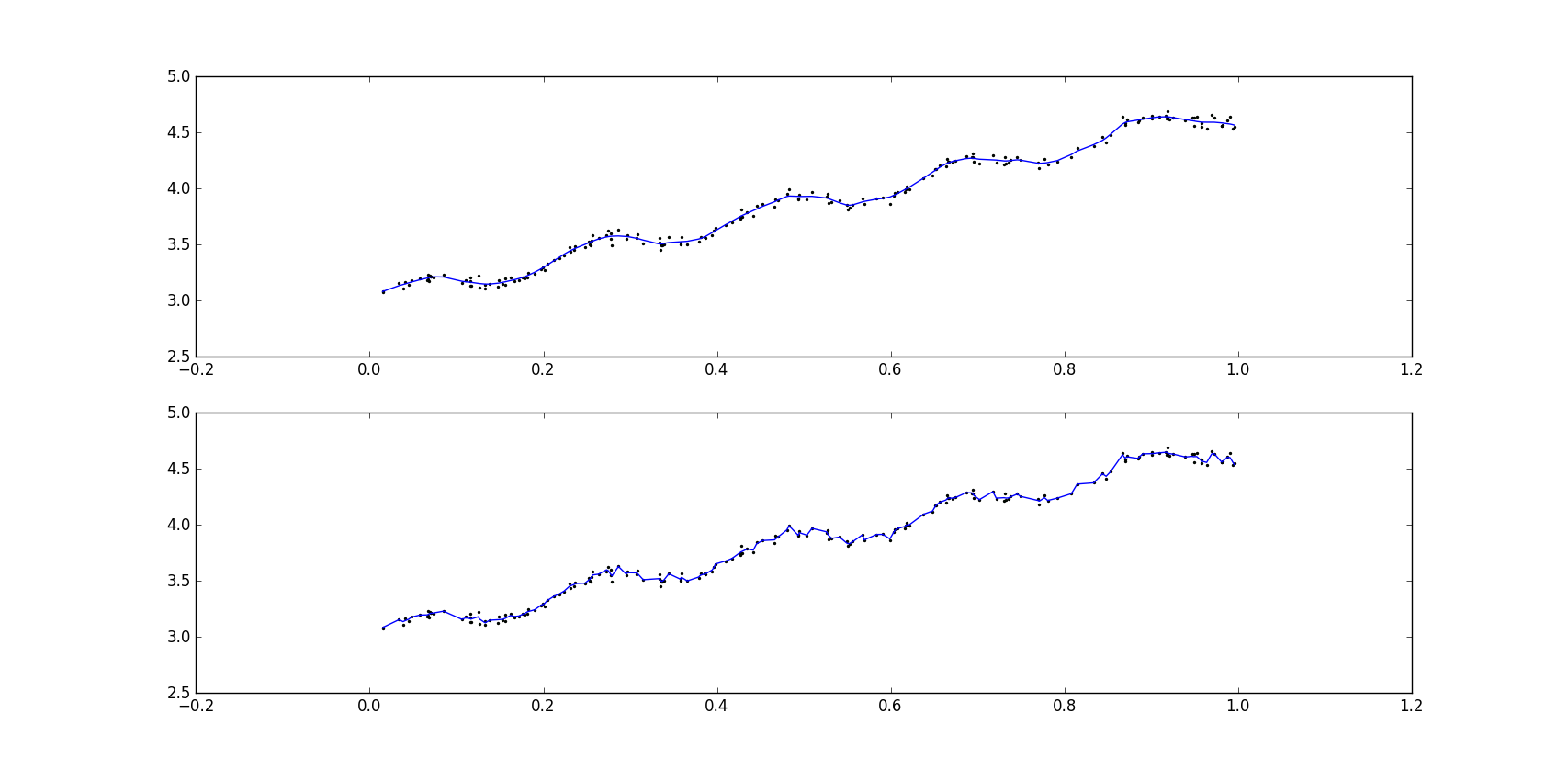
• 局部加权线性回归也存在问题，即增加了计算量。因为其对每个点做预测时都要使用整个数据集，虽然k=0.01时得到了很好的估计，但大多数数据点的权重接近0，如果避免这些运算，可以减少程序运行时间，从而缓解因计算量增加带来的问题。

预测鲍鱼年龄

• 向regression.py中加入下面代码，用于计算两个参数间误差的大小。可以看出，使用较小的核会得到较低的误差，但使用较小的核会造成过拟合，对新数据不一定能达到最好的预测效果。在新数据中，核大小等于10时误差最小，但核为10时的训练误差却是最大的。通过比较，简单线性回归达到了与局部加权线性回归相似的效果，因此必须在未知数据集上比较效果才能选取到最佳模型。

def rssError(yArr, yHatArr):
    return ((yArr - yHatArr)**2).sum()
>>> abX, abY = regression.loadDataSet('abalone.txt')
>>> yHat01 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
>>> yHat1 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1.0)
>>> yHat10 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10.0)
>>> regression.rssError(abY[0:99], yHat01.T)
56.782850757712595
>>> regression.rssError(abY[0:99], yHat1.T)
429.89056187011101
>>> regression.rssError(abY[0:99], yHat10.T)
549.11817088259465
>>> yHat01 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
>>> yHat1 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1.0)
>>> yHat10 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10.0)
>>> regression.rssError(abY[100:199], yHat01.T)
14772.633501680577
>>> regression.rssError(abY[100:199], yHat1.T)
573.5261441898798
>>> regression.rssError(abY[100:199], yHat10.T)
517.57119053849158
>>> ws = regression.standRegres(abX[0:99], abY[0:99])
>>> yHat = mat(abX[100:199]) * ws
>>> regression.rssError(abY[100:199], yHat.T.A)
518.63631532464785

缩减系数来“理解”数据

当数据特征数大于样本点，此时输入数据的矩阵X不是满秩矩阵，因此计算(X^T·X)^(-1)时会出错。为了解决该问题，引入“岭回归”（ridge regression）概念和lasso方法。

岭回归

• 简单说岭回归就是在矩阵X^T·X上增加一个λI从而使矩阵非奇异，进而能对X^T·X+λI求逆，其中矩阵I是一个m·m的单位矩阵。在这种情况下，回归系数的计算公式为(X^T·X+λI)^(-1)·X^T·y)。岭回归最先用来处理特征数多于样本数的情况，现在也用于在估计中加入偏差，从而得到更好的估计。这里通过引入λ来限制了所有w的和，通过引入该惩罚项，能够减少不重要的参数，称为“缩减”，缩减方法可以去掉不重要的参数，因此能更好的理解数据。

• 下面的代码包含计算回归系数的ridgeRegres函数和用于在一组λ上测试的ridgeTest函数。为了使用岭回归和缩减技术，首先要对数据标准化处理，使每维数据具有同样的重要性。具体的做法是所有特征都减去各自的均值并除以方差。代码中的λ以指数级变化，可以看出λ在去非常小的值和非常大的值时对结果造成的不同影响。

def ridgeRegres(xMat, yMat, lam = 0.2):
    xTx = xMat.T * xMat
    denom = xTx + eye(shape(xMat)[1]) * lam
    if linalg.det(denom) == 0.0:
        print "This matrix is singular, cannot do reverse"
        return
    ws = denom.I * (xMat.T * yMat)
    return ws

def ridgeTest(xArr, yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    yMean = mean(yMat, 0)
    yMean1 = mean(yMat, 1)
    print yMean, yMean1
    yMat = yMat - yMean
    xMeans = mean(xMat, 0)
    xVar = var(xMat, 0)
    xMat = (xMat - xMeans) / xVar
    numTestPts = 30
    wMat = zeros((numTestPts, shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat, yMat, exp(i-10))
        wMat[i,:] = ws.T
    return wMat
    
>>> abX, abY = regression.loadDataSet('abalone.txt')
>>> ridgeWeights = regression.ridgeTest(abX, abY)
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(ridgeWeights)
>>> plt.show()

• 上面代码最后的cpython交互部分代码给出了岭回归的回归系数变化图，如下。在最左边即λ最小时，可以得到所有系数的原始值（和线性回归一致），在最右边，系数全部缩减为0。在中间的某个值可以取得最好的预测效果。

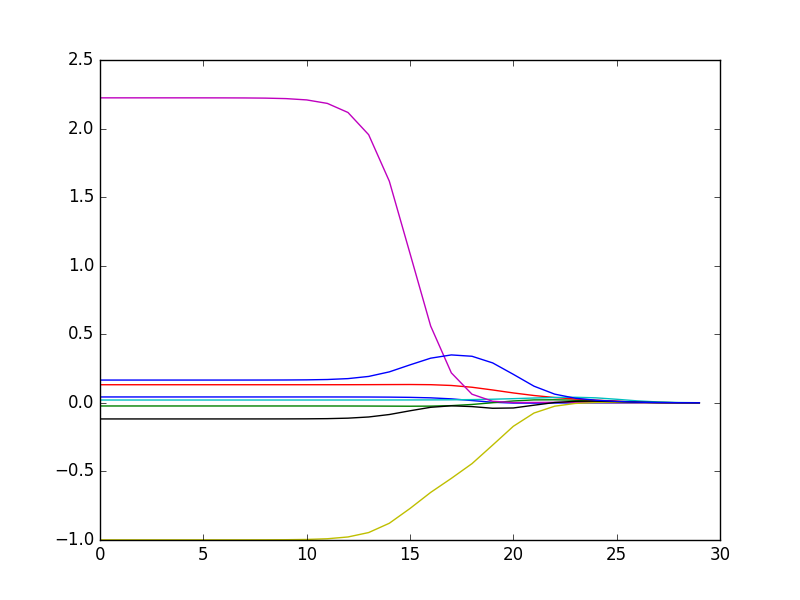
lasso

• 在增加约束∑w^2<=λ的情况下，普通的最小二乘法会得到与岭回归同样的公式，这个限制条件限定了所有回归系数的平方和不能大于λ。使用普通的最小二乘法回归在当两个或更多的特征相关时，可能会得出一个很大的正系数和一个很大的负系数。正是因为上面限制条件的存在，岭回归可以避免这个问题。与岭回归类似，另一个缩减方法lasso也对回归系数做了限定，但约束为∑|w|<=λ，这个约束条件用绝对值取代平方和。虽然形式变化不大，但结果差距明显。当λ足够小时，一些系数会因此被迫缩减到0，这个特性可以帮助我们更好地理解数据。在这个新的约束条件下求解回归系数极大的增加了计算复杂度，需要使用二次规划算法。

前向逐步回归

• 前向逐步回归算法可以得到与lasso差不多的效果，但更简单。它属于一种贪心算法，即每一步尽可能减少误差。一开始所有权重设为1，然后每一步的决策是对某个权重增加或减少一个很小的值。伪代码如下。

  • 数据标准化，使其满足0均值和单位方差
  • 在每轮迭代过程中：设置当前最小误差lowestError为正无穷。
  • 在每轮迭代过程中：对每个特征：增大或减小：改变一个系数得到新的W，计算新W的误差，如果误差Error小于当前最小误差lowestError，设置Wbest等于当前的W。
  • 返回Wbest

• 前向逐步线性回归函数 - regression.py。stageWise是逐步线性回归算法的实现，输入包括输入数据xArr和预测变量yArr，每次迭代要调整的步长eps和迭代次数numIt。函数首先将输入数据转换并存入矩阵，然后把特征按照均值为0方差为1进行标准化处理。之后迭代numIt次，更新最佳W矩阵。从运行得出的数据看出，w1和w6都是0，队结果没有任何影响，因此这两个特征很可能是不需要的。另外，在eps=0.01的情况下，一段时间后系数就已经在特定值之间来回震荡，这是因为步长太大，如第一个特征在0.04和0.05之间震荡。

def stageWise(xArr, yArr, eps=0.01, numIt = 100):
    xMat = mat(xArr); yMat = mat(yArr).T
    yMean = mean(yMat, 0)
    yMat = yMat - yMean
    xMat = regularize(xMat)
    m, n = shape(xMat)
    returnMat = zeros((numIt, n))
    ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
    for i in range(numIt):
        print ws.T
        lowestError = inf
        for j in range(n):
            for sign in [-1, 1]:
                wsTest = ws.copy()
                wsTest[j] += eps*sign
                yTest = xMat * wsTest
                rssE = rssError(yMat.A, yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i,:] = ws.T
    return returnMat

>>> regression.stageWise(xArr, yArr, 0.01, 200)
array([[ 0.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
       ...,
       [ 0.05,  0.  ,  0.09, ..., -0.64,  0.  ,  0.36],
       [ 0.04,  0.  ,  0.09, ..., -0.64,  0.  ,  0.36],
       [ 0.05,  0.  ,  0.09, ..., -0.64,  0.  ,  0.36]])

• 换用更小的步长，并和常规最小二乘法比较。

>>> regression.stageWise(xArr, yArr, 0.001, 5000)
array([[ 0.   ,  0.   ,  0.   , ...,  0.   ,  0.   ,  0.   ],
       [ 0.   ,  0.   ,  0.   , ...,  0.   ,  0.   ,  0.   ],
       [ 0.   ,  0.   ,  0.   , ...,  0.   ,  0.   ,  0.   ],
       ...,
       [ 0.043, -0.011,  0.12 , ..., -0.963, -0.105,  0.187],
       [ 0.044, -0.011,  0.12 , ..., -0.963, -0.105,  0.187],
       [ 0.043, -0.011,  0.12 , ..., -0.963, -0.105,  0.187]])
>>> xMat = mat(xArr); yMat = mat(yArr).T
>>> xMat = regression.regularize(xMat)
>>> yM = mean(yMat, 0)
>>> yMat = yMat - yM
>>> weights = regression.standRegres(xMat, yMat.T)
>>> weights.T
matrix([[ 0.0430442 , -0.02274163,  0.13214087,  0.02075182,  2.22403814,
         -0.99895312, -0.11725427,  0.16622915]])

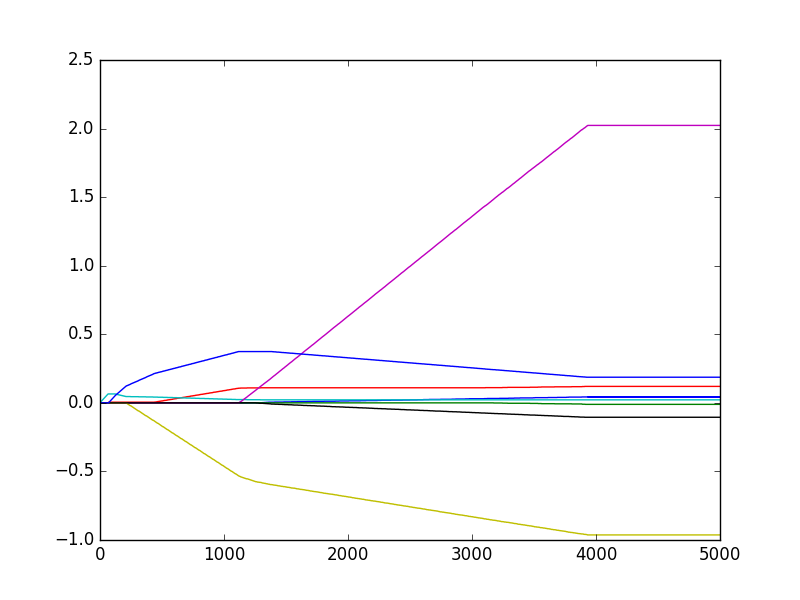
• 从数据可以看出，5000次迭代后，逐步线性回归算法和组常规的最小二乘法效果类似，使用0.001的ε值并经过5000次迭代的效果如下图。逐步线性回归算法的好处在于它可以帮助人们理解现有的模型并做出改进。当构建了一个模型后，可以运行该算法找出重要的特征，这样有可能及时停止那些不重要特征的收集。如果用于测试，该算法每100次迭代后就可以构建出一个模型，可以使用类似10折交叉验证的方法比较这些模型，选择误差最小的模型。当应用缩减方法（如逐步线性回归或岭回归）时，模型也就增加了偏差，与此同时减小了模型的方差。

权衡偏差与方差

• 当发现模型和测量值之间存在差异，说明出现了误差。当对复杂的过程进行简化时，会导致模型和测量值之间出现“噪声”或者误差，若无法理解数据的真是生成过程，也会导致差异发生。另外，测量过程本身也可能产生“噪声”。
• 如果降低核的大小，训练误差将变小，而测试误差则不一定。以模型复杂度为横轴，预测误差为纵轴，则训练误差的图象类似y = e^(-x)，而测试误差的图像类似y=(x-1)^2。使用缩减法将一些系数缩减成很小的值或直接缩减为0，这就减少了模型的复杂度。例子里有8个特征，消除其中两个既使模型易于理解，又降低了预测误差。
• 方差可以度量，取任意两个随机样本集，得出的回归系数都是不同的，这些回归系数间的差异大小就是模型方差大小的反应。偏差（预测值和真实值）和方差（不同回归系数间差异）折中的概念在机器学习十分流行且反复出现。

预测乐高玩具套装价格

• 用回归法预测乐高套装价格流程

  • 收集数据：使用Google Shopping的API。
  • 准备数据：从返回的json数据中抽取价格。
  • 分析数据：可视化并观察数据。
  • 训练算法：构建不同的模型，采用逐步线性回归和直接的线性回归模型。
  • 测试算法：使用交叉验证来测试不同的模型。

• 获取购物信息的函数searchForSet和setDataCollect，regression.py。searchForSet函数调用google购物api并保证数据抽取的正确性。初始休眠10秒防止短时间内过多的api调用。对得到的数据用简单的方法判断是否为二手套装（价格低于原始价格一半），并过滤掉这些信息。似乎现在这个URL已经404错误了，当然是挂了VPN的情况下。

def searchForSet(retX, retY, setNum, yr, numPce, origPrc):
    sleep(10)
    myAPIstr = 'AIzaSyD2cR2KFyx12hXu6PFU-wrWot3NXvko8vY'
    searchURL = 'https://www.googleapis.com/shopping/search/v1/public/products?key=%s&country=US&q=lego+%d&alt=json' % (myAPIstr, setNum)
    pg = urllib2.urlopen(searchURL)
    retDict = json.loads(pg.read())
    for i in range(len(retDict['items'])):
        try:
            currItem = retDict['items'][i]
            if currItem['product']['condition'] == 'new':
                newFlag = 1
            else:
                newFlag = 0
            listOfInv = currItem['product']['inventories']
            for item in listOfInv:
                sellingPrice = item['price']
                if sellingPrice > origPrc * 0.5:
                    print "%d\t%d\t%d\t%f\t%f" % \
                        (yr, numPce, newFlag, origPrc, newFlag, origPrc)
                    retX.append([yr, numPce, newFlag, origPrc])
                    retY.append(sellingPrice)
        except:
            print 'problem with item %d' % i

def setDataCollect(retX, retY):
    searchForSet(retX, retY, 8288, 2006, 800, 49.99)
    searchForSet(retX, retY, 10030, 2002, 3096, 269.99)
    searchForSet(retX, retY, 10179, 2007, 5195, 499.99)
    searchForSet(retX, retY, 10181, 2007, 3428, 199.99)
    searchForSet(retX, retY, 10189, 2008, 5922, 299.99)
    searchForSet(retX, retY, 10196, 2009, 3263, 249.99)

• 根据书上的结果，用常规最小二乘法得到的回归公式是55319.97-27.59*Year-0.00268*NumPieces-11.22*NewOrUsed+2.57*OriginalPrice，即售价和套装里的零部件数目和崭新程度成反比，显然不合常理。下面交叉验证测试岭回归。随机生成10组交叉验证的数据集，并在每组数据上调用岭回归产生的30组回归系数，最后选取使10组数据集误差均值最小的回归系数。最终的结果和常规最小二乘法没有太大差异，显然我们要寻找一个更易于理解的模型的期望没有达到。但我们可以查看岭回归过程中，回归系数在迭代中缩减的情况，因为系数是经过不同程度的缩减得到的，因此在特征非常多时，它可以指出哪些特征是必须的而哪些是不必要的。

def crossValidation(xArr, yArr, numVal = 10):
    m = len(yArr)
    indexList = range(m)
    errorMat = zeros((numVal, 30))
    for i in range(numVal):
        trainX = []; trainY = []
        testX = []; testY = []
        random.shuffle(indexList)
        for j in range(m):
            if j < m * 0.9:
                trainX.append(xArr[indexList[j]])
                trainY.append(yArr[indexList[j]])
            else:
                testX.append(xArr[indexList[j]])
                testY.append(yArr[indexList[j]])
        wMat = ridgeTest(trainX, trainY)
        for k in range(30):
            matTestX = mat(testX); matTrainX = mat(trainX)
            meanTrain = mean(matTrainX, 0)
            varTrain = var(matTrainX, 0)
            matTestX = (matTestX - meanTrain) / varTrain
            yEst = matTestX * mat(wMat[k,:]).T + mean(trainY)
            errorMat[i,k] = rssError(yEst.T.A, array(testY))
    meanErrors = mean(errorMat, 0)
    minMean = float(min(meanErrors))
    bestWeights = wMat[nonzero(meanErrors==minMean)]
    xMat = mat(xArr); yMat = mat(yArr)
    meanX = mean(xMat, 0); varX = var(xMat, 0)
    unReg = bestWeights/varX
    print "the best model from Ridge Regression is: \n" , unReg
    print "with constant term: ", -1*sum(multiply(meanX, unReg)) + mean(yMat)

回归预测数值型数据 总结

回归也是预测目标值的过程，但预测的目标是连续性变量。在回归方程中，求得特征对应的最佳回归系数的方法是最小化误差平方和。给定输入矩阵X，如果X^T·X的逆存在，则可使用标准回归法。标准回归法可能会出现欠拟合现象，如果在估计中引入一些偏差，就可以降低预测的均方误差，其中一个方法是局部加权线性回归。如果数据的样本数比特征数都要小，特征很可能高度相关，此时X^T·X必然不是满秩矩阵，无法求逆。此时可以考虑使用岭回归，岭回归是缩减法的一种，相当于为回归系数的大小增加了限制。另一种缩减法是lasso，可以用计算简便的逐步线性回归方法求得近似结果。缩减法可以看成是对一个模型增加偏差的同时减小方差，偏差方差折中可以帮助我们理解现有模型并做出改进。

---

参考文献： 《机器学习实战 - 美Peter Harrington》

原创作品，允许转载，转载时无需告知，但请务必以超链接形式标明文章原始出处(https://forec.github.io/2016/02/18/machinelearning8/) 、作者信息（Forec）和本声明。