Logistic回归根据现有数据对边界回归线建立回归公式,以此进行分类。训练分类器时的做法就是寻找最佳拟合参数,使用的是最优化算法。
Logistic回归和Sigmoid函数
- Logistic回归过程
- 准备数据:需要进行距离运算,数据类型为数值型,结构化数据格式最佳。
- 分析数据:任意方法。
- 训练算法:大部分时间用于训练,训练目的为了找到最佳的分类回归系统。
- 测试算法:训练步骤完成后分类将会很快。
- 使用算法:输入数据并将其转换为对应的结构化数值,之后基于训练好的回归系数可以对这些数值进行简单的回归计算,判定其属于哪个类别。
- Logistic回归优缺点
- 优点:计算代价不高,易于理解和实现
- 缺点:容易欠拟合,分类精度不高
- 使用数据类型:数值型和标称型
- Sigmoid函数:是近似海维塞德阶跃函数(单位阶跃函数),
σ(z)=1/(1+e^(-z))。当x为0时,Sigmoid(0)=0.5,随着x的增大减小,σ(x)将逼近1和0。当横坐标刻度足够大,Sigmoid看起来类似阶跃函数。我们将输入数据的每个特征乘以对应的回归系数,得到的结果相加,作为Sigmoid函数的参数,得到一个范围在0-1之间的数值,若大于0.5则归入1,小于0.5则归入0。因此Logistic回归可以被看成概率估计。
最佳回归系数确定
- 梯度上升法与梯度下降法类似,梯度上升算法用来求函数的最大值,梯度下降算法用来求函数的最小值。思想为要找到某函数的最大值,则沿着该函数的梯度方向探寻。梯度上升法到达每个点后会重新估计移动方向,循环迭代直至满足停止条件。对于线性回归系数,初始状态均为1,每次迭代的计算公式为
w:=w+α▽f(w),▽f(w)是在w处的梯度,α是沿梯度方向移动量大小,记为步长。该公式一直迭代执行,直到停止条件,比如迭代次数达到某个指定值,或误差达到指定精度。 使用梯度上升找到最佳参数,R为迭代次数,流程如下:
- 每个回归系数初始化为1
- 重复以下步骤R次:计算整个数据集的梯度,使用alpha*gradient更新回归系数的向量,返回回归系数
Code - gradAscent - logRegres.py
1 | def sigmoid(inX): # the array from numpy can be used as a single parameter |
- Code - loadDataSet - logRegres.py ,loadDataSet函数导入testSet.txt,返回数据矩阵和标签。gradAscent接收数据矩阵和标签,并返回生成的回归系数向量。
1 | def loadDataSet(): |
- Code - plotBestFit - logRegres.py
1 | def plotBestFit(weights): |
随机梯度上升
gradAscent函数迭代五百次,并且每次计算都要遍历整个数据集,对于大规模数据复杂度过高。改进方法为每次仅用一个样本点来更新回归系数,只在新样本到来时对分类器进行增量式更新,是在线学习算法。流程如下。
- 所有回归系数初始化为1
- 对数据集中的每个样本:计算该样本的梯度,使用alpha*gradient更新回归系数值
- 返回回归系数值
Code - stocGradAscent0 - logRegres.py,随机上升算法在200次迭代时的系数变化过程在《机器学习实战》82页,其中系数X2经过50次迭代后达到稳定,而系数1和0则需要更多次迭代。并且,在大的波动停止后,还有一些小的周期性波动,这源于数据中存在一些不能正确分类的样本点(数据集非线性可分),在每次迭代时会引发系统的剧烈震荡。
1 | def stocGradAscent0(dataMatrix, classLabels): |
- Improve - Code -stocGradAscent1 - logRegres.py,改进后的代码中,alpha每次迭代都会调整,这可以缓解高频波动,并且虽然alpha随着迭代次数减小,但永远不会减小到0(常数项存在),这样保证多次迭代之后新数据仍然对系数有影响。同样,这也避免了alpha的严格下降,避免参数的严格下降也常见于模拟退火算法等其他优化算法中。改进后的代码通过随机选取样本的方式更新回归系数,这样可以减少周期性波动。改进后的代码收敛速度更快,默认迭代次数150。
1 | def stocGradAscent1(dataMatrix, classLabels, numIter = 150): |
- 改进后的回归系数
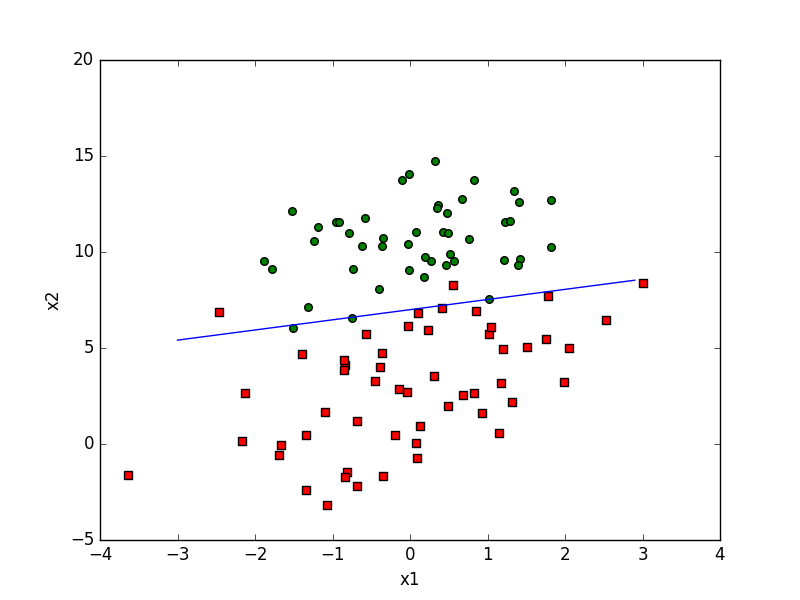
处理数据中的缺失值
- 假设有1000个样本和20个特征,若某传感器损坏导致一个特征无效,其余数据仍可用。
- 使用可用特征的均值填补缺失值
- 使用特殊值来填补确实值,如-1
- 忽略有缺失值的样本
- 使用相似样本的均值填补缺失值
- 使用另外的机器学习算法预测缺失值
对于Logistic回归,确实只用0代替可以保留现有数据,并且无需对算法进行修改。如果在测试数据集中发现某一条数据的类别标签已经缺失,Logistic回归的简单做法是将该数据丢弃,但如果采用类似kNN的方法则不太可行。
Code 用logistic回归从疝气病症预测病马死亡率 - logRegres.py
1 | def classifyVector(inX, weights): |
Matplotlib绘制
备份下列几份代码(来自《机器学习实战》的github),大致了解matplotlib绘制的基本方法。
- 绘制等高线 - plotGD.py
1 | import matplotlib |
- 生成图像如下
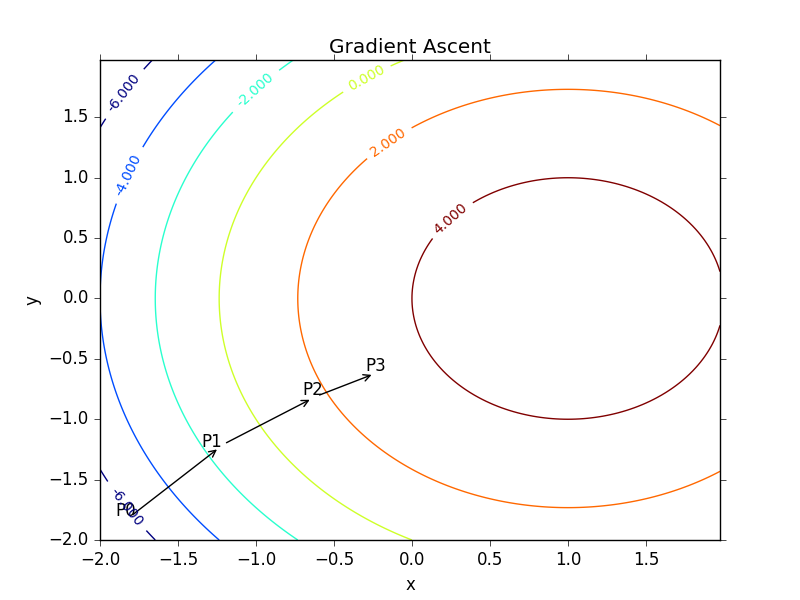
- 随机梯度上升过程中回归系数的变化 - plotGD.py
1 | from numpy import * |
- 生成图像如下
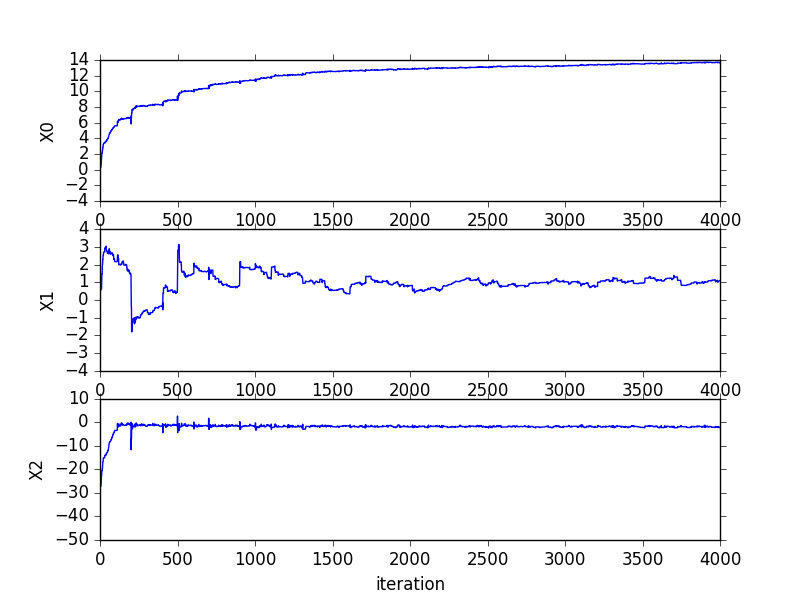
- 生成sigmoid函数 - sigmoidPlot.py
1 | import sys |
- 生成图像如下
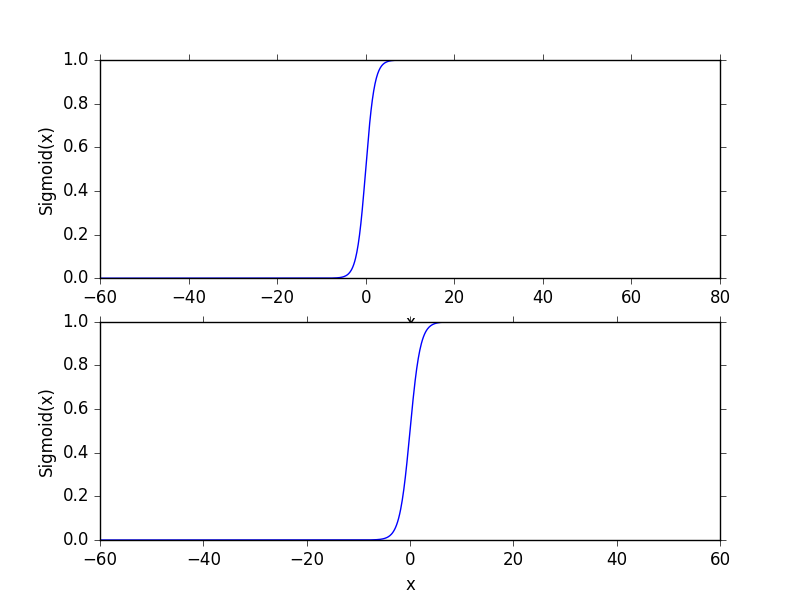
Logistic回归总结
Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数,求解过程可以由最优化算法完成。随机梯度上升算法可以简化梯度上升算法,获取几乎相同的效果,并且占用更少的计算资源,在新数据到来时完成在线更新,而不需要重新读取整个数据集。
参考文献: 《机器学习实战 - 美Peter Harrington》
原创作品,允许转载,转载时无需告知,但请务必以超链接形式标明文章原始出处(https://forec.github.io/2016/02/09/machinelearning5/) 、作者信息(Forec)和本声明。