最小生成树和最小树形图

2015-09-23

最小生成树的算法设计，以及实现的Prim和Kruskal算法。最小树形图的朱刘算法。

摘要

分析一下MST普适算法，加一些证明，帮助理解。

最小生成树

一个有V个顶点的无向连通图，其最小生成树是包含原图全部V个顶点，并且保持V个节点连通的，具有V-1条权值之和最小边的连通子图。（MST）

算法设计

贪心策略在求解MST时是可行的：要寻找最小生成树T，对于任意顶点u而言，在其相邻边的集合中，假设权值最小边是（u，v），而T中不包含（u，v），因此一定有另一条相邻边（u，v’）∈T且其权值大于（u，v），这意味着T不满足最小生成树的性质。根据定义，最小生成树只含有V-1条边，因此关键在于如何寻找不破坏性质而对整体而言权值相对更小的边。最小生成树包含图中所有顶点，因此从任一顶点开始搜索都可以获取到满足的MST，假设从顶点s开始，对于s紧邻的所有顶点遍历过后，一定会有一个顶点v，使得（s，v）的权值是所有s邻边中最小的，根据上面贪心策略的证明，（s，v）∈T。将构造过程中的顶点集合记为A，边集合记为E^s ，此时A = {s，v}，E^s = {（s，v）}，E^s ⊆T。

定义一些概念：无向图G =（V，E）的一个割（A，V - A）是对顶点集V的一个划分，当一条边（u，v）∈E并且其中一个顶点∈A，另一个顶点∈（V - A），称这条边（u，v）通过割（A，V - A）。如果一个边集E’满足其中任一边都不通过某个割，则说这个割不妨害边集E’。如果某一条边的权值是通过一个割的所有边中最小的，则称该边为通过这个割的一条轻边（可能会有多条轻边）。
接下来对E^s 继续扩充。显然，再向E^s 中加入任何直接或间接连接s，v的边都是无用的，称这些边为对E^s 不安全的边。可以添加的安全边必须满足一定条件，下面寻找这个条件。上一句已经表明：安全边首先必须通过割（A，V - A），否则是不安全的。根据贪心策略，应当在通过割的边中寻找最小边，因此定义里的轻边是符合这两个前提的。下面证明，通过割（A，V - A）的轻边是对E^s 安全的（显然，割（A，V - A）是不妨害E^s 的）：
- 假设T是包含E^s 的一棵最小生成树，并且T不包含轻边（u，v）（否则证明完成）。因为T不包含（u，v），所以向T中加入（u，v）将构成回路。因为（u，v）通过割（A，V - A），所以在T中存在另外一条边也通过割，假设这条边是（x，y），因为割不妨害E^s ，所以（x，y）不属于E^s 。在T中，除去任意一条边都会导致生成树变成两个子图，如果去掉（x，y），T将被分成两个子图（u到v的唯一通路断开），此时加入边（u，v）将使得T重新被连接，新的T’ = T - {（x，y）}∪{（u，v）}。接下来可以证明T’是一颗最小生成树。记ω（a，b）为边（a，b）的权值，因为（u，v）是轻边，所以ω（u，v）≤ ω（x，y），所以ω（T’）≤ ω（T）。又已知T是最小生成树，所以ω（T）≤ ω（T’）。因此T’是最小生成树。
- 下面证明（u，v）是E^s 的一条安全边。因为E^s ⊆T而（x，y）∉E^s ，故E^s ⊆T’。故E^s ∪{（u，v）}⊆T’。因为T’是最小生成树，所以（u，v）对E^s 是安全的。

整个流程。根据上面的证明，已经确定了加边的过程和依据。

Get-MST( G, ω ){
    E^s ← ∅
    while E^s hasn't formed a MST
        find a safe edge (u, v) for E^s
        E^s ← E^s ∪{（u，v）}
    return E^s
}

Prim算法

Prim算法又称为DJP算法，分别于1930年由捷克数学家沃伊捷赫·亚尔尼克（Vojtěch Jarník），1957年由美国计算机科学家罗伯特·普里姆（Robert C. Prim），1959年由艾兹格·迪科斯彻多次发现。下面的链接是Wiki上关于普里姆算法的描述。

算法描述

输入一个加权连通图G =（V，E）。
初始化一个顶点集Vn = {s}，s是集合V中的任一节点作为起点，边集En = {}为空。
重复下列操作直到V = Vn：
- 从集合E中选取（u，v），满足以下条件：u属于Vn且v不属于Vn，并且这样的（u，v）在E中权值最小，如果存在多条相同权值的边，任选其一。
- 将v加入Vn中，将边（u，v）边加入En中。
En为最小生成树包含的V-1条边的集合。

时间复杂度分析

邻接矩阵表示:采用邻接矩阵存储，每次寻找到权值最短的边需要O（V），一共需要O（V^2）。
采用邻接表+二叉堆，O（（V+E）logV）。因为对维护边的二叉堆每次操作需要logV，需要调整边E次，向En加边后删除最小元V次。
采用斐波那契堆+邻接表为O（E+VlogV），在连通图足够稠密时（E = Ω（VlogV）时），可以显著提高运行速度。

代码实现(邻接表+堆优化）

#include <stdio.h>
#include <stdlib.h>
#include <memory.h>

#define INF 0x7fffffff

struct edge
{
	int v, w, next;
}* edges;

int *h, *heap, *pos, *dist;
/*
 dist used to store the distance between Vn and V - Vn
 h[i] points to the position of first v satisfying (u,v)
 heap[] simulates a heap structure to store vertexs
 pos[u] counts the position of vertex u in heap[]
*/ 
int V, E, size, count;

void insert( int u, int v, int w ){
	edges[++count].v = v;
	edges[count].w = w;
	edges[count].next = h[u];
	h[u] = count;
}

void swap( int * a , int * b ){
	int temp = *a;
	*a = *b;
	*b = temp;
}

int Father( int u ){
	return u / 2;
}

int Left( int u ){
	return 2 * u;
}

int Right( int u ){
	return 2 * u + 1;
}

void heapUp( int u ){
	while ( u > 1 ){
		if ( dist[ heap[ Father(u) ] ] > dist[ heap[u] ] ){
			swap( pos + heap[ Father(u) ] , pos + heap[u]  );
			swap( heap + Father(u) , heap + u );
			u = Father(u);
		}
		else 
			break;
	}
}

void heapDown( int u ){
	while ( Left(u) <= size ){
		int child;
		if ( Left(u) == size || dist[ heap[ Left(u) ] ] < dist[ heap[ Right(u) ] ] )
			child = Left(u);
		else
			child = Right(u);
		if ( dist[ heap[u] ] > dist[ heap[child] ] ){
			swap( pos + heap[u], pos + heap[child] );
			swap( heap + u, heap + child );
			u = child;
		}			
		else 
			break;
	}
}

void push( int v, int w ){
	dist[v] = w;
	heap[ ++size ] = v;
	pos[v] = size;
	heapUp(size);
}

int pop(){
	int root = heap[1];
	swap( pos + heap[size], pos + heap[1]);
	swap( heap + (size--), heap + 1 );
	heapDown(1);
	return root;
}

void init(){
	int i, u, v, w;
	scanf( "%d %d", &V, &E );
	h = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	heap = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	pos = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	dist = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	memset( h, 0, sizeof(int) * ( V + 1 ) );
	memset( heap, 0, sizeof(int) * ( V + 1 ) );
	memset( pos, 0, sizeof(int) * ( V + 1 ) );
	memset( dist, 0, sizeof(int) * ( V + 1 ) );
	edges = ( struct edge * )malloc( sizeof( struct edge ) * ( 2 * ( E + 2) ) );
	for ( i = 1 ; i <= E ; i++ ){
		scanf( "%d %d %d", &u, &v, &w );
		insert( u, v, w );
		insert( v, u, w ); 
	}
	push( 1, 0 );
	for ( i = 2 ; i <= V ; i++ )
		push( i, INF );
}

int prim(){
	int i, v, ans = 0;
	for ( i = 1 ; i <= V ; i++ ){
		int front = pop();
		ans += dist[front];
		pos[front] = -1;
		for ( v = h[front] ; v != 0 ; v = edges[v].next ){
			int destination = edges[v].v;
			if ( pos[destination] != -1 && dist[destination] > edges[v].w ){
				dist[destination] = edges[v].w;
				heapUp( pos[destination] );
				heapDown( pos[destination] );
			}
		}
	}
	return ans;
}

int main(){
	init();
	printf( "%d\n", prim() );
	return 0;
}

代码给出最小生成树的权值和。如果需要记录E^s ，要额外建立一个数组e，在每次修改dist的时候维护e，或者在edge结构中加入一个flag域区分此边是否被选中，每次维护dist都要更新对应边的flag域。
运行示例：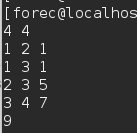

Kruskal算法

可以看出要优化Prim需要比较高的代码复杂度。Kruskal算法从E中选取V-1条边，其贪心策略简单并且易实现，完全基于上面算法设计的描述，只需要对边进行操作，并用并查集判断点之间的相交关系。采用快速排序的Kruskal时间复杂度为O（ElogE），适合稀疏图。如果不采用快速排序，改用优先队列维护Kruskal效率会更高（如果边比较多，会有很多无用边无需排序，只要取出优先队列前列的需要的MST边）。与Prim的区别在于：Kruskal中，E^s 是一个森林，加入集合E^s 的安全边总是连接G中的两个不同连通分支的最小权边；而在Prim中，E^s 一直只有一棵树，每次向E^s 中添加的安全边连接E^s 和一个不在树中的顶点的最小权边。

算法描述

对于无向连通图G =（V，E），先构造一个只含V个顶点，边集为空的子图G’，若将G’中各个顶点看成是各棵树上的根结点，则它是一个含有V棵树的一个森林。从E中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入G’，即将这两个顶点分别所在的两棵树合成一棵树；反之若该条边的两个顶点已落在同一棵树上，则跳过，取下一条权值最小的边再尝试。直至森林中只有一棵树，即G’中含有V-1条边。

代码实现（快速排序+并查集，边集数组存储）

#include <stdio.h>
#include <memory.h>
#include <stdlib.h>

typedef struct Edge{
	int u, v, w;
}edge;

int V, E;
int * f, * r;  // r[u] is the depth of the tree with the root u 
edge * edges;

int cmp( const void * a, const void * b ){
	return  ( (edge * ) a)->w - ( (edge *) b)->w;
}

int getFather( int x ){
	if ( f[x] != x )
		f[x] = getFather( f[x] );
	return f[x];
}

int isSame( int x, int y ){
	return getFather( x ) == getFather( y );
}

int setUnion( int x,int y ){
	int fx, fy;
	if ( ( fx = getFather(x) ) == ( fy = getFather(y) ) )
		return 1;
	if ( r[fx] > r[fy] )
		f[fy] = fx;
	else {
		f[fx] = fy;
		if ( r[fx] == r[fy] )
			r[fy]++;
	}
	return 0;
}

void init(){
	scanf( "%d %d", &V, &E );
	int i;
	edges = ( edge * ) malloc ( sizeof( edge ) * E );
	f = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	r = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	memset( r, 0, sizeof( int ) * ( V + 1 ) );
	for ( i = 0 ; i < E ; i++ )
		scanf( "%d %d %d", &edges[i].u, &edges[i].v, &edges[i].w );
	qsort( edges, E, sizeof( edge ), cmp );
	for ( i = 1 ; i <= V ; i++ )
		f[i] = i;
}

int Kruskal(){
	int i, e = 0, ans = 0;
	for ( i = 0 ; i < E && e < V - 1  ; i++ )
		if ( !isSame( edges[i].u, edges[i].v ) ){
			e++;
			ans += edges[i].w;
			setUnion( edges[i].u, edges[i].v );
		}
	if ( e != V - 1 )
		return -1;
	return ans;
}

int main()
{
	init();
	printf( "%d\n", Kruskal() );
	return 0;
}

最小树形图

上面的最小生成树针对无向加权连通图，在有向带权图中，指定一个特定的顶点root，求出一棵以root为根的有向生成树T，使得T中所有边的总权值最小，该问题称为最小树形图。以下均不考虑图中不存在最小树形图的情况（判断是否存在只要对图进行一次遍历即可确定）。

朱刘算法

朱刘算法是最小树形图的第一个算法，在1965年由朱永津和刘振宏提出，复杂度为O（VE）。

算法描述

对固定根root进行一遍DFS判断是否存在最小树形图。
为除了root之外的每个顶点选定一条最小的入边（用pre[u]记录顶点u最小入边的起点）。
判断2中构造的入边集合是否存在有向环，如果不存在，那么这个集合就是该图的最小树形图。
如果3中判断出现有向环，则消环缩点。设（u, v, w）表示从u到v的权为w的边。假设3中判断出的有向环缩为新顶点new，若u位于环上，并设环中指向u的边权是ω[u]。那么对于每条从u出发的边（u, v, w），在新图中连接（new, v, w），对于每条进入u的边（in, u, w），在新图中建立边（in, new, w-ω[u]）。新图里最小树形图的权加上旧图中被收缩的环的权和，就是原图中最小树形图的权值。重复2，3，4。
3中判断无有向环，返回权值。

其他：
- 如果没有指定固定根，可以增加一个虚拟根，并且为其增加V条边指向每个顶点，权值都为原图所有边权值之和加一，转化为固定根求解。
- 朱流算法只能求解最小总权值，无法求出路径（缩点后原顶点编号改变）。

代码描述（边集数组）

#include <stdio.h>
#include <stdlib.h>
#include <memory.h>

#define INF 0x7fffffff

int V, E;

typedef struct Edge{
	int u, v, w;
}edge;

int * in, * num, * pre, * father;
edge * edges;

void init(){
	int i;
	scanf( "%d %d", &V, &E );
	num = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	in = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	pre = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	father = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	edges = ( edge * ) malloc ( sizeof( edge ) * E );
	for ( i = 0 ; i < E ; i++ )
		scanf( "%d %d %d", &edges[i].u , &edges[i].v, &edges[i].w );

}

int Unidirectional_MST( int root ){
	int ans = 0;
	int i, u, v;
	while ( 1 ){
		for ( i = 1 ; i <= V ; i++ )
			in[i] = INF;
		for ( i = 0 ; i < E ; i++ ){			// 寻找最短边
			u = edges[i].u;
			v = edges[i].v;
			if ( edges[i].w < in[v] && u != v ){
				in[v] = edges[i].w;
				pre[v] = u;
			}
		}
		for ( i = 1 ; i <= V ; i++ )			// 判断有无孤立点
			if ( in[i] == INF && i != root )
				return 0;
		int count = 1;
		memset( num, 0, sizeof( int ) * ( V + 1 ) );
 		memset( father, 0, sizeof( int ) * ( V + 1 ) );
 		in[root] = 0;
 		for ( i = 1 ; i <= V ; i++ ){
 			ans += in[i];
 			v = i;
 			while ( father[v] != i && num[v] == 0 && v != root ){	// 寻找环
 				father[v] = i;
 				v = pre[v];
 			}
 			if ( v != root && num[v] == 0 ){	// 缩点
 				for ( u = pre[v] ; u != v ; u = pre[u] )
 					num[u] = count;
 				num[v] = count++;
 			}
 		}
 		if ( count == 1 )
 			break;
 		for ( i = 1 ; i <= V ; i++ )	// 顶点重编号
 			if ( num[i] == 0 )
 				num[i] = count++;
 		for ( i = 0 ; i < E ; i++ ){	// 维护与环相连的边
 			v = edges[i].v;
 			edges[i].u = num[edges[i].u];
 			edges[i].v = num[edges[i].v];
 			if ( edges[i].u != edges[i].v )
 				edges[i].w -= in[v];
 		}
 		V = count - 1;	// 更新当前顶点数量和新根
 		root = num[root];
 	}
 	return ans;
}
int main()
{
	init();
	printf( "%d\n", Unidirectional_MST(1) );
	return 0;
}

流程展示

盗了一张图，演示最小树形图的构造流程，并以此为样例试运行上面的代码。
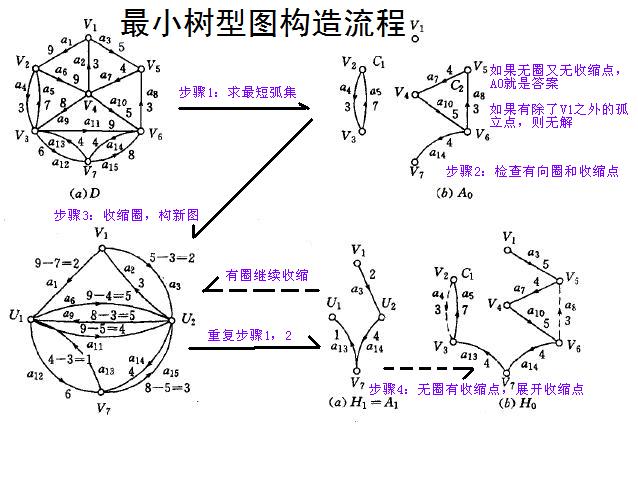
运行结果如下：

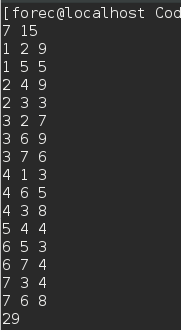
1986年Tarjan等提出的复杂度更好的算法

1986年， Gabow, Galil, Spencer和Tarjan提出了一个复杂度更好的实现，其时间复杂度为O(E+VlogV)。相关资料比较少，以后会把这里补上。

原创作品，允许转载，转载时无需告知，但请务必以超链接形式标明文章原始出处(https://forec.github.io/2015/09/23/Graph-Algorithms4/) 、作者信息（Forec）和本声明。

Code

摘要

最小生成树

算法设计

Prim算法

算法描述

时间复杂度分析

代码实现(邻接表+堆优化）

Kruskal算法

算法描述

代码实现（快速排序+并查集，边集数组存储）

最小树形图

朱刘算法

算法描述

代码描述（边集数组）

流程展示

1986年Tarjan等提出的复杂度更好的算法