图的概念和存储方式

2015-09-12

图的概念和术语、标准表示方式以及其他存储方式。

摘要

图的概念和术语

一个图（Graph）是表示物件与物件之间的关系的方法，是图论的基本研究对象。一个图看起来是由一些小圆点（称为顶点或结点）和连结这些圆点的直线或曲线（称为边）组成的。（From Wikipedia）

给定图G=（V，E），其中V代表|V|，指的是图中的顶点数，E代表|E|，指的是图中的边数。通过这两个参数描述一个图的规模。以下均使用二元组的定义方式定义G，对于映射关系复杂的使用三元组G=（V，E，I），I为关联函数，将E中的每个元素映射到V。
基本术语
- 阶（Order）：图G中V的大小称为G的阶。
- 子图（Sub-Graph）：图G’称为G的子图，当V(G’)包含于V(G)，并且E(G’)包含于E(G)。
- 生成子图（Spanning Sub-Graph）：满足V(G’)=V(G)的子图。
- 度（Degree）：一个顶点的度是指与该顶点相关联的总边数，顶点v的度记作d(v)。在G中：∑d(v) = 2|E|。
- 出度（Out-Degree）和入度（In-Degree）：有向图中，顶点v的出度是以v为起点的边的数量，入度相反。
- 自环（Loop）：一条边的起点和终点是同一个顶点。
- 路径（Path）：从顶点u到顶点v的一条路径是指经过一个边的序列（u，v1），（v1，v2），（v2，v3），……，（vn，v），若u = v则该路径是闭的，否则是开的。若v1，v2，……，v两两不等，则该路径为简单路径，又称轨道（Track）（允许u=v），闭的轨道称为圈（Cycle）。
- 行迹（Trace）：若路径P（u，v）中各边都不相同则该路径为u到v的一条行迹。闭的行迹称为回路（Circuit）。
- 距离（Distance）：从u到v的最短路径存在时，该最短路径的长度为从u到v的距离。不存在路径时，距离为∞。
- 桥（Bridge）：若去掉一条边使得整个图不连通，则该边称为桥。
有向图：图中顶点之间的路径存在方向，A->B的路径存在不等于B->A的路径也存在。
无向图：图中顶点之间的路径是双向的。
完全图：若图中每一对不同顶点恰有一条边相连，则称为完全图。完全图是每对顶点之间都恰连有一条边的简单图。无向完全图的边数E=V×(V-1)/2。有向完全图E=V×(V-1)。
连通图和连通分量：在无向图中，若从顶点A到顶点B有路径，则称A和B连通。若图中任意两个顶点之间都连通，则称该图为连通图，否则，称该图为非连通图，其中的极大连通子图称为连通分量（极大指该子图中包含的顶点个数在所有连通子图中极大）。有向图的最大连通子图称为该有向图的强连通分量。任何连通图的连通分量只有一个（其自身）。
团：团是G的一个完全子图，如果一个团不是其他任何一个团的真子集，则该团为G的极大团。顶点最多的极大团是G的最大团。

标准表示方式

概念

表示一个图的标准方法有邻接表和邻接数组，这两种方法都可以同时用于有向图和无向图。通常采用邻接表表示法，它用来存储稀疏图（E远小于V^2）更紧凑。当遇到稠密图或必须很快判断两个顶点间是否存在边时使用邻接数组表示法（如Floyd算法）。

邻接表：G=（V，E）的邻接表由一个包含|V|个列表的数组D组成，每个顶点对应数组中的一个列表。对于顶点u∈V，当存在一条路径u->v（v∈V），则D[u]中包含v或指向v的指针。邻接表中的顶点可以按任意顺序存储。当G是有向图，邻接表D的长度为E，G是无向图，邻接表D的长度为2E（一条边需要在两个方向存储）。邻接表修改后可以支持多种图的变体，有很强的适应性，但若要确定图中边（u，v）是否存在只能经过线性时间搜索。
邻接数组：在G=（V，E）中，将各个顶点按某种方式编号为1，2，3，……，|V|，之后通过一个|V|×|V|的矩阵A存储，当（u，v）∈E，Auv = 1，否则Auv = 0。若为加权图，则可以用权值和∞代替1和0。这种表示方法在O(1)的时间内得到u，v之间的关系，但需要较大的存储空间。
以下是无向图和有向图使用上述两种方式的表示形式。

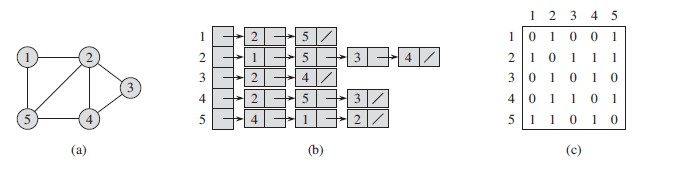
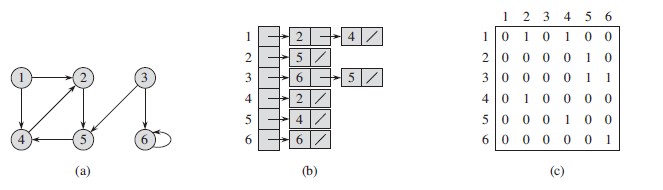
从上面图可以看出，邻接矩阵A关于主对角线对称，即A = A^T ，在无向图的一些应用中可以只存储主对角线和主对角线以上的部分，减少一半的存储空间。

完整代码

邻接表表示法（无向加权图）

/*
 * @author Forec
 * Test Adjacency List
 */
#include <stdio.h>
#include <stdlib.h>
struct Node{
	int w;
	int v;
	struct Node * next;
};

typedef struct Node node;

void insert( int u, int v, int weight, node ** List ){
	node * temp;
	temp = ( node * )malloc( sizeof( node ) );
	temp->v = v;
	temp->w = weight;
	temp->next = List[u];
	List[u] = temp;			// Add node v to the head of list[u]
	temp = ( node * )malloc( sizeof( node ) );
	temp->v = u;
	temp->w = weight;
	temp->next = List[v];
	List[v] = temp;			// Add node u to the head of list[v]
}

void print( node ** List, int V ){
	int i;
	node * temp;
	for ( i = 1 ; i <= V ; i++ ){
		printf( "%d", i );
		temp = List[i];
		while ( temp != NULL ){
			printf( "->%d(%d)", temp->v, temp->w );
			temp = temp->next;			
		}
		putchar('\n');
	}
}

int main(){
	int V, E, u, v, w;
	int i;
	scanf( "%d %d", &V, &E );
	node ** Adj = ( node ** )malloc( sizeof( node * ) * ( V + 1 ) );
	for ( i = 1 ; i <= V ; i++ )
		Adj[i] = NULL;
	for ( i = 0 ; i < E ; i++ ){
		scanf( "%d %d %d", &u, &v, &w );
		insert( u, v, w, Adj );
	}
	print( Adj, V );
	return 0;
}

邻接矩阵表示法（无向加权图）

/*
 * @author Forec
 * Test Adjacency Matrix
 */
#include <stdio.h>
#include <stdlib.h>

#define INF 0x7fff

int Min( int a, int b ){
	return a < b ? a : b;
}

int Max( int a, int b ){
	return a > b ? a : b;
}

int main(){
	int V, E, u, v, w;
	int i, j;
	scanf( "%d %d", &V, &E );
	int ** Mat = ( int ** )malloc( sizeof( int * ) * ( V + 1 ) ); 
	for ( i = 1 ; i <= V ; i++ ){
		Mat[i] = ( int * )malloc( sizeof( int ) * ( i + 1 ) );
		for ( j = 1 ; j < i ; j++ )
			Mat[i][j] = INF;
		Mat[i][i] = 0;
	}
	for ( i = 0 ; i < E ; i++ ){
		scanf( "%d %d %d", &u, &v, &w );
		Mat[Max( u, v )][Min( u, v )] = w;
	}
	for ( i = 1 ; i <= V ; i++ ){
		for ( j = 1 ; j <= i ; j++ )
			printf( "%d\t",Mat[i][j]);
		putchar('\n');
	}
	return 0;
}

其他存储方式

边集数组

边集数组利用几个一维数组存储图中的所有边。

举例，输入数据：
1 4
1 3
3 2
5 2
1 5
上面输入完成后，边集数组如下

	1	2	3	4	5
source	1	1	3	5	1
destination	4	3	2	2	5

容易看出，边集数组只是简单的存储每条边的信息，如果需要存储权值只需要再加上一个域。在边集数组中查找一条边或一个顶点的度都需要扫描整个数组，所以其时间复杂性为O（e）。边集数组适合那些对边依次进行处理的运算，不适合对顶点的运算和对任一条边的运算。

前向星和链式前向星

前向星是特殊的边集数组，把边集数组中的每一条边按照起点排序，如果起点相同就按照终点排序，之后用Len[i]记录以i为起点的边共有多少条，以Head[i]记录这Len[i]条边中第一条在前向星数组的哪个位置。举例，输入数据：
1 4
1 3
3 2
5 2
1 5
在上面的输入完成后，对其排序得到
编号 1 2 3 4 5
起点 1 1 1 3 5
终点 3 4 5 2 2

此时Len和Head数组分别为
Head Len
1 1 3
2 -1 0
3 4 1
4 -1 0
5 5 1
前向星需要先对边集数组排序，用快排需要O（NlogN）复杂度，计数排序也需要O（M）的预处理时间。
链式前向星
不需要排序，建立边结构体
1
2
3
4
5
struct Edge{
int next;
int to;
int weight;
}
其中，edge[i].to为第i条边的终点，edge[i].next表示与第i条边同起点的下一边在Edge数组中的位置，edge[i].weight为权值。此外还需要数组head，初始化为-1。head[i]表示以i为起点的第一条边的存储位置，利用链式前向星存储时，head[i]记录的位置是按输入顺序最后一条以i为起点的边所存储的位置。插入边代码如下。
1
2
3
4
5
6
7
// initialize cnt 0
void insert( int u, int v, int w ){
edge[cnt].to = v;
edge[cnt].weight = w;
edge[cnt].next = head[u];
head[u] = cnt++;
}
按照上面前向星的例子，插入结束后得到的edge数组如下
i edge[i].to edge[i].next edge[i].w head
1 4 -1 - head[1] = 0
2 3 0 - head[1] = 1
3 2 -1 - head[3] = 2
4 2 -1 - head[5] = 3
5 5 1 - head[1]= 4
遍历时按输入顺序的倒序遍历，for ( int i = head[u] ; i >= 0 ; i = edge[i].next )。

十字链表

对于邻接矩阵，处理稀疏图资源利用效率不高，可以结合邻接表的思想，链式表示稀疏矩阵。当然其应用不局限于矩阵，一切具有正交关系的结构都可以使用十字链表存储。
row col value
right down

以上是十字链表的结构，row和col分别表示当该元素使用邻接矩阵存储时所在的行数和列数。value是元素值（权值），down指向了当用邻接矩阵存储时，同一列中下一个非0元素所在的位置，right指向了当用邻接矩阵存储时，同一行中下一个非0元素所在的位置。
每行/列设一个表头结点（结构与元素结点相同），与down/right构成循环链表，即第i列头结点的down指向该列上第1个非0元素，第i行头结点的right指向该行第1个非0元素，第i列/行上最后一个结点的down/right指向该列/行的头结点。如果某列/行中没有非0元素，则令它的头结点down/right域指向自己。
可以额外设置一个表头指针数组，指向每行/列的表头节点。
代码实现十字链表的结构和插入

#include <stdio.h>
#include <stdlib.h>
struct Node{   
    int row, col, value;   
    struct Node *right, *down;   
};
typedef struct Node OLNode;
typedef struct Node * OLink;   

typedef struct{   
    OLink *rowHead;
    OLink *colHead;   
    int row, col, len;
}CrossList;
   
void CreateCrossList( CrossList * List ){   
    int row, col, len, i, u, v, w;   
    OLink p, q;  
    scanf( "%d %d %d", &row, &col, &len ); /* row, col分别为十字链表模拟数组的行数和列数，len为非0元素数目 */   
    List->row = row;   
    List->col = col;   
    List->len = len;   
    List->rowHead = ( OLink * )malloc( ( row+1 ) * sizeof( OLink ) );
    List->colHead = ( OLink * )malloc( ( col+1 ) * sizeof( OLink ) ); // 应检查是否overflow 
    for( i = 0; i < row + 1 ; i++ )
		List->rowHead[i] = NULL;      
    for( i = 0; i < col + 1 ; i++ )
		List->colHead[i] = NULL;
    for( i = 0 ; i < len ; i++ ){ 
		scanf( "%d %d %d ", &u, &v, &w );
		p = ( OLink )malloc( sizeof( OLNode ) ); // 实际使用要检查溢出
		p->row = u;
		p->col = v;
		p->value = w;
		if ( List->rowHead[u] == NULL ){
			List->rowHead[u] = p;
			p->right=NULL;
		}
		else{
			for( q = List->rowHead[u] ; q->right != NULL && q->right->col < v ; q = q->right );
			p->right = q->right;
			q->right = p;
		}
		if(List->colHead[v] == NULL){
			List->colHead[v] = p;
			p->down = NULL;
		}
		else{
			for( q = List->colHead[v] ; q->down != NULL && q->down->row < u; q = q->down );
			p->down = q->down;
			q->down = p;
		}
	}
}

原创作品，允许转载，转载时无需告知，但请务必以超链接形式标明文章原始出处(https://forec.github.io/2015/09/12/Graph-Algorithms1/) 、作者信息（Forec）和本声明。

i	edge[i].to	edge[i].next	edge[i].w	head
1	4	-1	-	head[1] = 0
2	3	0	-	head[1] = 1
3	2	-1	-	head[3] = 2
4	2	-1	-	head[5] = 3
5	5	1	-	head[1]= 4

编号	1	2	3	4	5
起点	1	1	1	3	5
终点	3	4	5	2	2

	Head	Len
1	1	3
2	-1	0
3	4	1
4	-1	0
5	5	1

row	col	value
right	down

Code

摘要