Code

LCA和RSA

Tarjan离线求解LCA和RSA加密算法。

Tarjan离线求解LCA

LCA（Least Common Ancestors），最近公共祖先，即在有根树中寻找到两个结点u，v距离和最短的结点，亦即离根最远的结点。

  • 算法基于DFS和并查集，时间复杂度由DFS的V和查询次数M决定，O（V+M）。在下面给出的代码样例中采用链式结构存储树，采用邻接表结构双向存储查询端点，也可以通过两个边集数组实现。

  • 算法流程：

    • 初始化：设置par数组（并查集），par[i] = i。离线所有查找请求，存储于无向图邻接表中。
    • 从根结点开始tarjan（DFS），对于每次新探求到的顶点u，对照每个查询请求（u，v），判断这条询问请求中的另一个结点v是否被搜索过。如果v尚未被搜索则暂时跳过该条请求（在我的样例中将这条请求留到了（v，u）处理），如果v已经被搜索过，则LCA（u，v）= Find（v），这里的Find是并查集操作。
    • 搜索并处理u包含的所有子树（每棵子树搜索完成意味着所有子树内的LCA询问都已经被解决）。在v的所有子树被搜索完成后，回溯时合并祖先，将所有自v处搜索出的顶点的par值设为u。
    • tarjan所有结点。
    • 核心部分的伪代码
1
2
3
4
5
6
7
8
9
tarjan(u)
     vis[u] <- true
     for each (u, v) in questions
         if vis[v]
             ans(u, v) <- Find(v)
     for each (u, v) in tree
         if !vis[v]
             tarjan(v)
             par[v] <- u

  • 对LCA（u，v）= Find（v）给出证明：因为v在遍历到u（当前结点）前被遍历过，而又由某个结点拓展到u，所以以最近公共祖先为根并且包含v的子树已经被搜索过，若有一个从当前结点u到结点v的查询，这时当前这棵子树的祖先就是最近公共祖先（注意当前的含义，当对v的搜索不断回溯时，Find（v）的值会在不断变化）。

  • 样例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <stdio.h>
#include <memory.h>
#include <stdlib.h>

typedef struct Node {
	int num;
	struct Node * left, * right;
}node;

typedef struct granode{
	int v;
	int ans;
	struct granode *next;
}granode; 

int V, E, Q;
int * vis, * par;
node * tree, * root = NULL;
granode ** list;

int Find( int u ){
	return par[u] == u ? u : Find( par[u] );
}

void insert( int u, int v ){
	granode * temp = ( granode * ) malloc ( sizeof( granode ) );
	temp->v = v;
	temp->next = list[u];
	list[u] = temp;
}

void init(){
	scanf( "%d %d %d", &V, &E, &Q );
	int i, father, child, u, v;
	tree = ( node * ) malloc ( sizeof( node ) * ( V + 1 ) );
	par = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	vis = ( int * ) malloc ( sizeof( int ) * ( V + 1 ) );
	list = ( granode ** ) malloc ( sizeof( granode* ) * ( V + 1 ) );
	memset( vis, 0, sizeof( int ) * ( V + 1 ) );
	for ( i = 1 ; i <= V ; i++ ){
		tree[i].num = i;
		tree[i].left = tree[i].right = NULL;
		list[i] = NULL;
		par[i] = i;
	}
	for ( i = 0 ; i < E ; i++ ){
		scanf( "%d %d", &father, &child );
		vis[child] = 1;
		if ( tree[father].left == NULL )
			tree[father].left = tree + child;
		else 
			tree[father].right = tree + child;
	}
	for ( i = 1 ; i <= V ; i++ )
		if ( !vis[i] )
			root = tree + i;
	memset( vis, 0, sizeof( int ) * ( V + 1 ) );
	for ( i = 1 ; i <= Q ; i++ ){
		scanf( "%d %d", &u, &v );
		insert( u, v );
		insert( v, u );
	}
}

void tarjan( node * n ){
	vis[ n->num ] = 1;
	int u = n->num;
	granode * temp = list[u];
	while ( temp != NULL ){
		if ( vis[ temp->v ] )
			temp->ans = Find( temp->v );
		temp = temp->next;
	}
	if ( n->left != NULL )
		if ( !vis[ n->left->num ] ){
			tarjan( n->left );
			par[ n->left->num ] = u;
		}
	if ( n->right != NULL )
		if ( !vis[ n->right->num ] ){
			tarjan( n->right );
			par[ n->right->num ] = u;
		}
}

void print(){
	int i;
	for ( i = 1 ; i <= V ; i++ ){
		granode * temp = list[i];
		while ( temp != NULL ) {
			if ( temp->ans )
				printf( "%d %d %d\n", i, temp->v, temp->ans );
			temp = temp->next;
		}
	}
}

int main(){
	init();
	printf("Root : %d\n",root->num );
	tarjan( root );
	print();
	return 0;
}
  • 运行结果
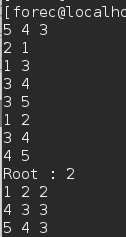
    LCA的Tarjan离线算法演示

RSA

选取两个不同的大素数p、q，并计算N = p×q，选取小素数d，并求出e = ~d，使 d × e ≡ 1 mod (p-1)(q-1)。对于任意明文 A < N有密文B =A^d mod N，解密时A = B^e mod N。因此d和~d形成了非对称密钥关系，使用公钥d加密，私钥e解密，即使第三方获取了密文B、公钥d和模数N，因为目前的RSA大多以大于1024位的大数为基础，因此对N进行素数因子分解近似不可能（不考虑量子算法），因此无法获取p，q，也就无法推算e。

大数运算

目前多为32和64bit编译器，对于1024位以上的大数运算通常将其作为数组处理。如果选取十进制，2^1024会产生一个长度300多位的数组，对于四则运算的任何一种操作都需要在两个数百位的数组上进行，效率非常低，并且将其转换成二进制非常麻烦。通常的改进方法是将大数用n进制数组表示，这里的n为2的幂，对32bit系统可以取n = 2 ^ 32（0x100000000），将1024位大数用该进制表示即为32位，每一位的取值是2^32进制的0～0xffffffff。这刚好是32位系统中long的长度。此时对该数组进行的任意运算所需的循环规模不超过32次，并且因为进制是2的次幂，与二进制的转换非常容易。

  • 存储方式：例如0xffffffff ffffffff，转换成十进制是18446744073709551615，格式类似于十进制中的99，十六进制中的0xFF。而0x00000001 00000000 00000000，转换成十进制是18446744073709551615 + 1 = 18446744073709551616，格式类似十进制的100，十六进制的0x0100。在数组中，i从0到n分别按由低位到高位的顺序存储。对于一个数组A表示的大数，其值通过如下方式计算：for i from 0 to n { ans <- ans + A[i] × base ^ i }。显然各个数字间的运算中间结果可能超出32位长度，因此需要64位的数据（long long，__int 64）类型存储（部分32位编译系统不支持64位，可使用2^16进制，并将32位数据类型用来存储中间结果；或者将2^32进制改成4×2^28进制，也就是0x40000000进制，这样两个数字运算最大结果为0x3fffffff × 0x3fffffff，不超过0xffffffffffffff，可以用double类型存储，但不能将中间结果简单的拆分成高位和低位）。

假设存在大数A和B，A.length和B.length表示各自长度，base = 0x100000000，0 <= A[i],B[i] < base。

  • 加法：处理进位情况和长度变化即可 
1
2
3
4
5
6
7
8
__int64  temp;
int pre = 0, len = max( A.length, B.length );
for ( i = 0 ; i <= len ; i++ ){
	temp = A[i] + B[i] + pre;
	res[i] = temp % 0x100000000;
	pre = temp / 0x100000000;
}
res.length = pre == 0 ? len : len + 1;
  • 减法：对中间结果是负数的需要借位 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int pre = 0;
int len = max( A.length, B.length );
for ( i = 0 ; i <= len ; i++ ){
	res[i] = A[i] - B[i] - pre;
	if ( res[i] >= 0 )
		pre = 0;
	else {
		res[i] += 0x100000000;	// 借位
		pre = 1;
	}
}
res.length = len;
while ( res[res.length] == 0 )
	res.length--;		//去除大数前端多余的0
  • 乘法：竖式运算，假设B.length < A.length，则res[i] = Sum{ A[i-j] × B[j], j from 0 to B.length }。res.length初始可以设置为A.length + B.length - 1，考虑到进位，最后可以根据情况增加一位。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
__int temp;
int pre = 0;
res.length = A.length + B.length - 1;
for ( i = 0 ; i <= res.length ; i++ ){
	temp = pre;
	for ( j = 0 ; j <= B.length ; j++ ){
		if ( i >= j && i <= j + A.length ){
			temp += A[i-j] * B[j];		// 竖乘
			res[i] = temp % 0x100000000;
			pre = temp / 0x100000000;
		}
	}
}
if ( pre )
	res[++res.length] = pre;	// 最高位进位
  • 除法：通过蒙哥马利算法可以通过移位操作代替除法求得模乘运算的结果

米勒·拉宾算法

  • 算法流程
    • 根据RSA中的N计算出一个奇数M，使得N = 1 + M × 2^r 。
    • 选择一个小于N的随机数C，对于任意的i < r，如果C^( ( M × 2^i ) % N) == N - 1或者C^M % N == 1，则N通过随机数C的测试。
    • 重复上一步五次，如果全部通过则判定N为素数

若N通过一次测试，则N为合数的概率为25%，当N通过t次测试，N为合数的概率为0.25^t。t为5时N为素数的概率已经大于99.9%。实际操作中通常用300个小素数对N进行测试，如果N通过小素数测试再使用米勒·拉宾测试，提高测试速度。

欧几里德方程

根据辗转相除法，当gcd(a,b) = 1，有sa + tb = 1。将求解a和b的gcd过程写出，逆向即可求得~b，使得b×~b ≡ 1（mod a）。

  • 辗转相除法的逆运算
    求解gcd（101,4620），有如下：
    4620 = 45 × 101 + 75
    101 = 1 × 75 + 26
      75 = 2 × 26 + 23
      26 = 1 × 23 + 3
       3 = 1 × 2 + 1
       2 = 2 × 1
    对上述操作求逆操作，为：
    1 = 3 - 1 × 2
      = 3 - 1 ×（23 - 7 × 3）= -1 × 23 + 8 × 3
      = -1 × 23 + 8 ×（26 - 1 × 23）= 8 × 26 - 9 × 23
      = 8 × 26 - 9 ×（75 - 2 × 26）= -9 × 75 + 26 × 26
      = -9 × 75 + 26 ×（101 - 1 × 75）= 26 × 101 - 35 × 75
      = 26 × 101 - 35 ×（4620 - 45 × 101）= -35 × 4620 + 1601 × 101
  • 下列代码传入的参数r最后为求得的~b。
1
2
3
4
5
6
7
8
9
10
void get( int a, int b, int *l, int *r){	/* 逆向欧几里得求 1 = st + qa */ 
	if ( a % b == 1 ){
		*l = 1;
		*r = -a / b;
	}
	else {
		get( b, a % b, l, r );
		(*r) = (*r) * ( - a / b ) + *l; 				/*  r为求得的modular  */ 
	}	
}
  • 非递归的代码如下( sa + tb = 1 )，返回的t即为~b。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int get( int a, int b ){
	int t = 0, s = 1, temp;
	while ( b ! = 0 ){
		temp = s;
		s = t - s * b / a;
		t = temp;
		temp = b;
		b = a % b;
		a = temp;
		if ( t < 0 )
			t += a;
	}
	return t;
}

Montgomery幂模算法

Montgomery（蒙哥马利）算法的优点在于减少了取模的次数，并且用移位取代除法。举例：进制base = 13，对于32 = 2 × 13 + 7。要求32×13^k mod 7的值，可以对32进行如下操作：32 = 32 + 7 × q，这样不影响取模的结果。当32 + 7 × q是13的整数倍的时候就可以用移位操作除以13，直到求出结果。

  • 伪代码
1
2
3
4
5
6
7
8
9
func() a^b mod c
	res <- 1
	pow <- b
	while a > 0
		pow <- ( pow * pow ) mod c
		if a & 1 = 1		// 以二进制为例，对于n进制有同样的增值运算
			res <- ( res * pow ) mod c
		a >> 1			// 对于任意进制同样移位
	return res

原创作品，允许转载，转载时无需告知，但请务必以超链接形式标明文章原始出处(https://forec.github.io/2015/09/10/Algorithms-Must1/) 、作者信息（Forec）和本声明。

分享到