强连通分量

求强连通分量的Tarjan算法和Kosaraju算法。

摘要

• 求强连通分量的Tarjan算法
• Kosaraju算法

求强连通分量的Tarjan算法

几年前搞NOIP的时候就已经有很多漂亮的blog介绍tarjan算法，其中byvoid的那篇非常简洁明了，并且给出了C语言的代码，但是大部分blog都没有对tarjan中的一些技巧给出详细的证明。ccf这两年正在推广的一个软件能力认证，上周第五次测试的题目里就有tarjan的模板题。现在重写一下tarjan，对一些地方给出证明。我个人认为多数blog里对Tarjan过程的图片展示适得其反，因此这里不会通过图片演示算法流程。关于强连通分量等的概念，在前面两篇： 图的概念和术语，边的分类。

算法描述

• Tarjan算法以DFS为基础，Tarjan生成的每棵深度优先树都是一个强连通子图，注意是强连通子图而非强连通分量，在byvoid的blog里并没有对这两个概念进行区分，但其所提供的代码可以得到所有的强连通子图，只需要分别计算一下图中顶点数目即可。因为对每个顶点Tarjan一次，并且需要遍历每条边，整个时间复杂度为O（V+E）。
• 下面是详细过程：
  1. 定义一个Stack，在遍历整棵树的时侯储存节点。
  2. 定义DFN[u]为顶点u的时间戳（在深度优先搜索中使用的数组d[u]和这里的dfn[u]是一个数组，都记录第一次访问顶点u时的时间），定义LOW[u]为u或u的子树能够向前追溯到的最早的栈中顶点的时间。如果不明白LOW数组记录的是什么，对照代码和后面的证明就可以理解。
  3. 按照DFS_Visit(u)的方式访问，不同的是每次对u的邻接顶点v访问时（即有一条有向边（u，v）），根据v的状态的不同予以区分。在深度优先搜索中，我们用白，灰和黑三种颜色表示顶点的不同状态，其中白色表示第一次访问，灰色表示已经访问但可能还有邻接顶点是白色，黑色表示该顶点所有的邻接顶点都是非白色的。在Tarjan中，对u的每个邻接顶点v，如果v是白色的（未访问过），则先对v用Tarjan，直到以v为根的子树访问完成后，返回顶点u，此时需要更新顶点u的LOW值：Low[u] = min( Low[u], Low[v] )，这根据定义（LOW[u]为u或u的子树能够向前追溯到的最早的栈中顶点的时间）就可以看懂：因为v是第一次被访问，所以v在u的子树中，Low[v]如果小于Low[u]，则说明以v为根的子树可以追溯到更早的栈中顶点，因此u或u的子树能够向前追溯的最早栈中顶点的时间就需要更新。
  4. 如果3中的v是灰色的，说明顶点v此刻正在栈中。在边的分类中，我写过反向边的辨别方法，即对于有向边（u，v），如果第一次访问这条边时，v是灰色，则（u，v）是一条反向边。此时需要更新Low[u]的值：Low[u] = min( Low[u], DFN[v] )。由定义知，DFN[v]记录的是第一次访问到顶点v的时间，因为（u，v）是反向边，因此u是v子树中的一个顶点，又因为v在栈中，因此v是u可以回溯到的某个栈中顶点，如果顶点v的时间戳早于之前记录的low[u]，就可以更新low[u]的值。
  5. 如果3中的v是黑色的（正向边或者交叉边），不需要操作，因为正向边意味着v在此前已经被访问过，并且遍历过所有以与之可到达的顶点为根的子树，其low值无法更改，而交叉边意味着v和u不属于同一个强连通子图。
  6. 与u相邻的所有顶点遍历过后，判断u是否是一个构成强连通子图的优先搜索树的根：判断条件是if ( low[u] == dfn[u] )。首先根据定义，dfn[u]一定不会小于low[u]，因为顶点u至少可以构成一个只含有u一个顶点的优先搜索树，也就是回溯到自身。如果可以回溯到栈中更早的顶点，就会有dfn[u] > low[u]。当dfn[u] = low[u]时，顶点u就是某个强连通子图的根：当dfn[u]和low[u]相等，意味着u所能够向上寻找的顶点是其自身，而这时从栈顶到u的所有元素都是以u为根的子树的顶点，所以栈中u以上的顶点都可以通过u直接或间接到达，而栈中u以上的顶点的low值都为u，也就意味着他们都可以直接或间接回溯到顶点u。因此从栈顶到u的所有元素可以弹出，这些元素组成一个强连通子图。
  7. 通过上面过程可以看出，当有环时，整个环上的顶点的low值是统一的（根的low值），即这些相同low值的顶点属于同一个强连通子图。在弹栈的过程中记录每个强连通子图中顶点个数，就可以得到强连通分量。

代码

• 邻接表（C语言）

#include <stdio.h>
#include <stdlib.h>
#include <memory.h>

#define WHITE 0
#define GRAY 1
#define BLACK 2

struct Node {
	int v;
	struct Node * next;
};

typedef struct Node node;

int min( int x,int y ){
	return x < y ? x : y;
}

void insert( node ** graph, int u, int v ){
	node * temp = ( node * )malloc( sizeof( node ) );
	temp->v = v;
	temp->next = graph[u];
	graph[u] = temp;
}

int V, E, time;
int * dfn, * low, * vis;
int * S, top;

void Tarjan( node ** graph, int u ){
	dfn[u] = low[u] = ++time;
	S[top++] = u;
	vis[u] = GRAY;
	node * temp = graph[u];
	while ( temp != NULL ){
		if ( vis[temp->v] == WHITE ){
			Tarjan( graph, temp->v );
			low[u] = min( low[u], low[temp->v] );
		}
		if ( vis[temp->v] == GRAY )
			low[u] = min( low[u], dfn[temp->v] );
		temp = temp->next;
	}
	vis[u] = BLACK;
	if ( dfn[u] == low[u] ){
		while ( S[--top] != u )
			printf("%d ", S[top] );
		printf( "%d\n", u );
	}
}

void Tarjan_Graph( node ** graph ){
	dfn = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	low = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	vis = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	S = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	memset( vis, 0, sizeof( int ) * ( V + 1 ) );
	int i;
	for ( i = 1 ; i <= V ; i++ )
		if ( vis[i] == WHITE )
			Tarjan( graph, i );
}

int main(){

	int i, u, v;
	scanf( "%d %d", &V, &E );
	node ** graph = ( node ** )malloc( sizeof( node * ) * ( V + 1 ) );
	for ( i = 1; i <= V ; i++ )
		graph[i] = NULL;
	for ( i = 0 ; i < E ; i++ ){
		scanf( "%d %d", &u, &v );
		insert( graph, u, v );
	}
	Tarjan_Graph( graph );
	return 0;
}

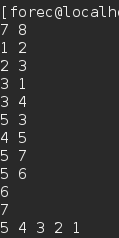
• 运行结果
  

---

Kosaraju算法

Kosaraju算法比Tarjan更容易理解，完全基于DFS，时间复杂度也是O（V+E）。算法导论中介绍的求强连通分量的算法就是Kosaraju。

算法描述

Kosaraju通过对原图和原图的转置（有向边（u，v）全部替换为有向边（v，u））分别进行有序的DFS获取强连通子图。这里摘录一段Wiki关于Kosaraju的描述：

1. Let G be a directed graph and S be an empty stack.
2. While S does not contain all vertices: Choose an arbitrary vertex v not in S. Perform a depth-first search starting at v. Each time that depth-first search finishes expanding a vertex u, push u onto S.
3. Reverse the directions of all arcs to obtain the transpose graph.
4. While S is nonempty: Pop the top vertex v from S. Perform a depth-first search starting at v. The set of visited vertices will give the strongly connected component containing v; record this and remove all these vertices from the graph G and the stack S. Equivalently, breadth-first search (BFS) can be used instead of depth-first search.

• 从上面的描述中第2步可以看出，对原图第一次DFS过程和对dag求拓扑序列的过程一致，得到的S栈看起来存放的就是拓扑序列。不过这里的图不是dag，而拓扑排序必须应用于dag。因为图中存在反向边，S中的序列就不一定满足拓扑排序中的偏序。这些反向边是构成强连通子图的关键，因此Kosaraju通过对图的转置进行DFS来突出这些反向边。原图转置（第3步）后，原本的反向边全部成为了正向边。对转置后的图按上述“不严格的拓扑序列”逆序（因为存储结构是栈，弹栈的过程产生的是不严格拓扑序列的逆序）DFS（第4步），这时的每棵深度优先树就是一个强连通子图。
• 证明1：要证明对原图的转置按“不严格的拓扑序列”进行DFS得到的深度优先树是强连通子图，只需要证明这棵树中任意两个顶点都是强连通的，对于Kosaraju算法而言，就是证明在原图的转置中，如果按照不严格拓扑序列DFS（u）可以访问到v，那么u和v是强连通的。
  1. 因为在原图的转置中对u搜索可以访问到v，因此一定存在一条从u到v的路径，也就是在原图中存在一条从v到u的路径，这意味着：在原图中，顶点u是顶点v的后裔。
  2. 证明在原图的转置中也存在从v到u的路径（也就是原图中存在一条从u到v的路径）：因为DFS（u）可以访问到v，所以“不严格拓扑序列”的逆序（S的弹栈）中，顶点u在顶点v之前，也就是在“不严格拓扑序列”中，顶点v出现在顶点u之前。这等价于：在原图中，或者1.顶点u在顶点v之前加入了DFS的堆栈（d[u] < d[v]），而顶点v先完成，并弹出到了“不严格拓扑序列”当中，顶点u在完成对其所有可到达邻接顶点的扫描后弹出到“不严格拓扑序列”中，或者2.顶点u在顶点v扫描完成后才加入DFS的堆栈（d[v] < d[u]）。因为原图中顶点v比顶点u先完成DFS，根据上一篇文章中有关的深度优先搜索的性质和条件1，原图的DFS过程中f[v] < f[u]，这里根据1和2可能出现两种情况（根据括号定理，要么不相交，要么包含）：1. d[u] < d[v] < f[v] < f[u]，2. d[v] < f[v] < d[u] < f[u]。根据括号定理和条件1，如果是第二种情况，v和u的区间互不相交，而原图中u是v的后裔，矛盾，所以只能是第一种情况。根据后裔区间嵌套定理，此时原图中v是u的后裔，证毕。
• 证明2：所有强连通子图都会被搜索到。这等价于推翻存在一对顶点（u，v）可互相到达，但不属于同一个强连通子图的情况。通过反证法：假设存在这样的（u，v），显然经过DFS后，其中一个点一定在另一个点拓展出的搜索树中。根据对称性，假设v在u拓展出的搜索树中，则在DFS过程中，v会在u之前弹出系统栈。假设命题不成立，就必须有一棵搜索树包含了v且不包含u，假设这棵搜索树的根是s：如果s比u先出栈，根据括号定理只能有d[s] < d[v] < f[v] < f[s] < d[u] < f[u]或者d[u] < d[s] < f[s] < f[u]，后者显然意味着s是u的后裔，而前者会在访问v的时候搜索到顶点u，因此s只能比u后出栈，即d[u] < f[u] < d[s] < f[s]或者d[s] < d[u] < f[u] < f[s]。后者显然意味着u是s的后裔，而前者因为（u，v）由已知可以互达，则从u拓展出的搜索树会在s之前搜索到v。综上，假设不成立，命题成立。
• 优势：按照Kosaraju算法求出来的强连通子图虽然比Tarjan稍慢，但得到的强连通子图是拓扑顺序的，因为对原图转置的DFS是按照不严格拓扑序列的逆序进行的，注意这里关系的转化。

代码

• 邻接表（C语言）

#include <stdio.h>
#include <stdlib.h>

#define WHITE 0
#define GRAY 1
#define BLACK 2

struct Node {
	int v;
	struct Node * next;
};

typedef struct Node node;

void insert( node ** graph, int u, int v ){
	node * temp = ( node * )malloc( sizeof( node ) );
	temp->v = v;
	temp->next = graph[u];
	graph[u] = temp;
}

int V, E, time;
int * vis, * list;
int * S, top;

void Dfs_Visit( node ** graph, int u ){
	printf( "%d ", u );
	vis[u] = GRAY;
	node * temp = graph[u];
	while ( temp != NULL ){
		if ( vis[temp->v] == WHITE )
			Dfs_Visit( graph, temp->v );
		temp = temp->next;
	}
	vis[u] = BLACK;
	S[top++] = u;
}

void Dfs( node ** graph ){
	int i;
	top = 0;
	for ( i = 1; i <= V ; i++ )
		vis[i] = 0;
	for ( i = 1 ; i <= V ; i++ )
		if ( vis[ list[i] ] == WHITE ){
			Dfs_Visit( graph, list[i] );
			putchar('\n');
		}
}

void init(){
	vis = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	S = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	list = ( int * )malloc( sizeof( int ) * ( V + 1 ) );
	int i;
	for ( i = 1 ; i <= V ; i++ )
		list[i] = i;
}

int main(){

	int i, u, v;
	scanf( "%d %d", &V, &E );
	node ** graph1 = ( node ** )malloc( sizeof( node * ) * ( V + 1 ) );
	node ** graph2 = ( node ** )malloc( sizeof( node * ) * ( V + 1 ) );
	for ( i = 1; i <= V ; i++ )
		graph1[i] = NULL;	
	for ( i = 1; i <= V ; i++ )
		graph2[i] = NULL;
	init();
	for ( i = 0 ; i < E ; i++ ){
		scanf( "%d %d", &u, &v );
		insert( graph1, u, v );
		insert( graph2, v, u );
	}
	Dfs( graph1 );
	for ( i = 1 ; i <= V ; i++ )
		list[i] = S[--top];
	printf( "Ans :\n" );
	Dfs( graph2 );
	return 0;
}

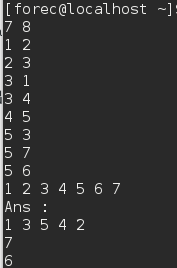
• 运行结果
  

---

原创作品，允许转载，转载时无需告知，但请务必以超链接形式标明文章原始出处(https://forec.github.io/2015/09/19/Graph-Algorithms3/) 、作者信息（Forec）和本声明。