机器学习笔记（Chapter 12 - FP-growth算法）

FP-growth算法基于Apriori构建，先将数据集存储在FP树内，再发现频繁项集，速度通常快于Apriori两个数量级以上。FP-growth只需要对数据库扫描两次，而Apriori需要对每个潜在的频繁项集扫描一次数据集。Apriori算法拓展性更好，可以用于并行计算。

FP树

• FP-growth算法速度优于Apriori，但实现相对困难，在某些数据集上性能会下降，适用于标称型数据。FP代表频繁模式，FP-growth算法将数据存储在FP树中。
• FP树通过链接来连接相似元素，被连接的元素项可以看成一个链表。与搜索树不同的是，一个元素项可以在FP树中出现多次，FP树会存储项集的出现频率，而每个项集以路径的方式存储在树中（类似字典树），存在相似元素的集合会共享树的一部分。树节点上给出集合中的单个元素及其在序列中的出现次数，路径会给出该序列的出现次数。
• 下表是用来生成下面示例的FP树的数据。

  生成FP树的事务数据样例

  事务ID	事务中的元素项
  001	r, z, h, j, p
  002	z, y, x, w, v, u, t, s
  003	z
  004	r, x, n, o, s
  005	y, r, x, z, q, t, p
  006	y, z, x, e, q, s, t, m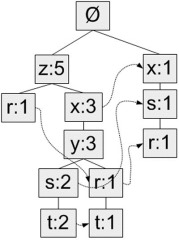

  
  

构建FP树

• 为FP树建立新的数据类，定义如下，fpGrowth.py。

class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue
        self.count = numOccur
        self.nodeLink = None
        self.parent = parentNode
        self.children = {}

    def inc(self, numOccur):
        self.count += numOccur

    def disp(self, ind = 1):
        print ' '*ind, self.name, ' ', self.count
        for child in self.children.values():
            child.disp(ind+1)

• 除了FP树外，还需要一个头指针表headerTable来存储FP树中元素第一次出现的位置和该元素的总数。上例中FP树的headerTable如下。
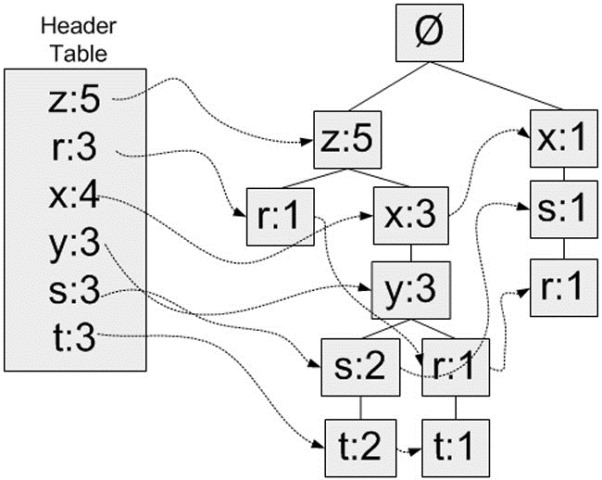
• 构造FP树过程如下：第一次遍历数据集会获得每个元素项的出现频率，之后去掉不满足最小支持度的元素项。再下一步构建FP树，读入每个项集并将其添加到一条路径中，若路径不存在则新建。每个事务都是一个无序集合，为了保证相同元素项只出现一次，需要对每个过滤后的事务中的元素项排序后再添加到树中，排序基于元素项的绝对出现频率由大到小开始。构造过程如下图。
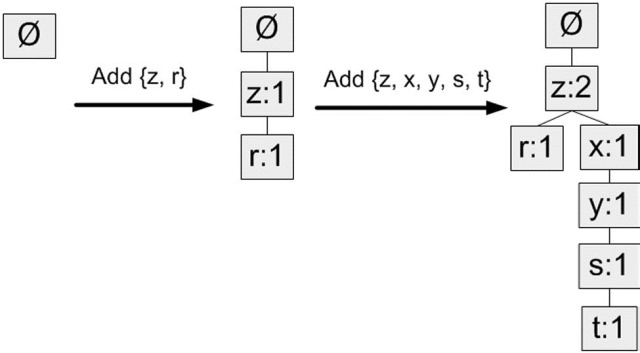
• 建树代码如下。函数createTree使用处理好的数据集和最小支持度作为参数，返回建好的FP树和FP树的headerTable。函数updateTree输入参数为一个项集、当前的FP树、当前FP树的headerTable和当前项集出现次数，updateTree将这个项集插入到当前的FP树中，具体实现是如果这个项集只有一个元素，那么如果这个元素已经存在FP树中，就增加它的count值，否则为它在当前FP树下新分配一个节点，并更新headerTable，如果这个项集不止一个元素，那么对剩下的元素递归调用updateTree。updateHeader是updateTree的子函数，用来更新headerTable，确保节点链接指向树中该元素项的每个实例。

def createTree(dataSet, minSup = 1):
    headerTable = {}
    for trans in dataSet:
        for item in trans:
            headerTable[item] = headerTable.get(item, 0) + dataSet[trans]
    for k in headerTable.keys():
        if headerTable[k] < minSup:
            del(headerTable[k])
    freqItemSep = set(headerTable.keys())
    if len(freqItemSep) == 0: return None, None
    for k in headerTable:
        headerTable[k] = [headerTable[k], None]
    retTree = treeNode('Null Set', 1, None)
    for tranSet, count in dataSet.items():
        localD = {}
        for item in tranSet:
            if item in freqItemSep:
                localD[item] = headerTable[item][0]
        if len(localD) > 0:
            orderedItems = [v[0] for v in sorted(localD.items(),\
                key = lambda p: p[1], reverse = True)]
            updateTree(orderedItems, retTree, headerTable, count)
    return retTree, headerTable

def updateTree(items, inTree, headerTable, count):
    if items[0] in inTree.children:
        inTree.children[items[0]].inc(count)
    else:
        inTree.children[items[0]] = treeNode(items[0], count, inTree)
        if headerTable[items[0]][1] == None:
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:
            updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
    if len(items) > 1:
        updateTree(items[1::], inTree.children[items[0]], headerTable, count)

def updateHeader(nodeToTest, targetNode):
    while (nodeToTest.nodeLink != None):
        nodeToTest = nodeToTest.nodeLink
    nodeToTest.nodeLink = targetNode

• 建树使用的数据集是处理过原始数据得到的一个字典。

def loadSimpDat():
    simpDat = [['r', 'z', 'h', 'j', 'p'],
               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
               ['z'],
               ['r', 'x', 'n', 'o', 's'],
               ['y', 'r', 'x', 'z', 'q', 't', 'p'],
               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return simpDat

def createInitSet(dataSet):
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1
    return retDict

• 上面代码对simpDat建立的FP树如下。

>>> simpDat = fpGrowth.loadSimpDat()
>>> initSet = fpGrowth.createInitSet(simpDat)
>>> myFpTree, myHeaderTab = fpGrowth.createTree(initSet, 3)
>>> myFpTree.disp()
  Null Set   1
   x   1
    s   1
     r   1
   z   5
    x   3
     y   3
      s   2
       t   2
      r   1
       t   1
    r   1

从FP树中挖掘频繁项集

从FP树获取频繁项集的步骤如下：从FP树中获取条件模式基，利用条件模式基构建一个条件FP树，迭代上面两步，直到树包含一个元素项为止。

抽取条件模式基

• 对于保存在headerTable中的每一个元素项，他们自身都是一个长度为一的频繁项集，首先要获得其对应的条件模式基。条件模式基是以所查找元素项为结尾的路径集合，每条路径都是一条前缀路径。例如在最初的FP树例子中，元素r的前缀路径是{x,s}、{z,x,y}和{z}，而这每一条前缀路径都对应一个计数值，计数值等于起始元素项的计数值，这里就是r出现的次数（1次）。这些前缀路径会被用来构建条件FP树，因为headerTable中包含了每个元素第一次出现的位置，因此可以通过headerTable遍历每个元素并且上溯整棵树到根节点。
• 函数ascendTree用来迭代上溯整棵树，findPrefixPath用来找到参数basePat对应的所有条件模式基，期间不停调用ascendTree。

def ascendTree(leafNode, prefixPath):
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)

def findPrefixPath(basePat, treeNode):
    condPats = {}
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink
    return condPats

>>> fpGrowth.findPrefixPath('r', myHeaderTab['r'][1])
{frozenset(['x', 's']): 1, frozenset(['z']): 1, frozenset(['y', 'x', 'z']): 1}

创建条件FP树

• 对于每一个频繁项都要创建一棵条件FP树，使用条件模式基作为输入数据，用相同的建树代码构建条件树，之后递归地发现频繁项、发现条件模式基，并且继续构造条件树，直到条件树中没有元素。
• 函数mineTree对参数inTree代表的FP树进行频繁项集挖掘。首先对headerTable中出现的单个元素按出现频率从小到大排序，之后将每个元素的条件模式基作为输入数据，建立针对当前元素的条件树，如果生成的这棵条件树仍有元素，就在这棵条件树里寻找频繁项集，因为prefix参数是在递归过程中不断向下传递的，因此由最初的headerTable中的某个元素x衍生出的所有频繁项集都带有x。

def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    bigL = [v[0] for v in sorted(headerTable.items(), key = lambda p: p[1])]
    for basePat in bigL:
        newFreqSet = preFix.copy()
        newFreqSet.add(basePat)
        freqItemList.append(newFreqSet)
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
        myCondTree, myHead = createTree(condPattBases, minSup)
        if myHead != None:
            print 'conditional tree for: ', newFreqSet
            myCondTree.disp(1)
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)

• mineTree函数递归过程稍微复杂，可以通过下面这幅图（链接是图的原作者）来了解。在mineTree的for basePat in bigL中，当前的basePat是t的情况下的递归过程。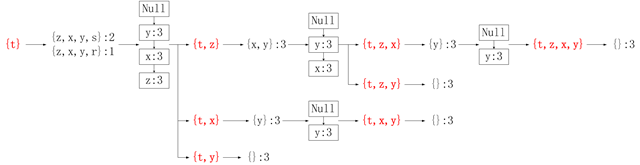下面是代码运行时以t为basePat情况下的部分输出。

>>> freqItems = []
>>> fpGrowth.mineTree(myFpTree, myHeaderTab, 3,set([]), freqItems)
conditional tree for:  set(['t'])
  Null Set   1
   y   3
    x   3
     z   3
conditional tree for:  set(['x', 't'])
  Null Set   1
   y   3
conditional tree for:  set(['z', 't'])
  Null Set   1
   y   3
    x   3
conditional tree for:  set(['x', 'z', 't'])
  Null Set   1
   y   3

在Twitter源中发现关键词

• 使用python-twitter库，链接是源代码和Twitter API文档，最好直接阅读python-twitter在github上源代码中的api.py文件。使用API需要从twitter开发服务网站获得两个app开发证书集合。
• 函数getLotsOfTweets处理OAuth认证并从twitter获取搜索相关的1400条推文。textParse将获取到的推文处理，mineTweets对每条推文调用textParse，生成FP树并返回所有频繁项集组成的list。注释掉的api.VerifyCredentials()可以查看api是否授权成功。作者写书时候的api现在已经更新了，GetSearch方法里的per_page和page参数都已经取消，现在是count和since_id，另外有一个since参数是起始日期，格式XXXX-XX-XX，因为是用pip安装的python-twitter，和github上的源码不同步，这里没有用。

import twitter
from time import sleep
import re

def getLotsOfTweets(searchStr):
    CONSUMER_KEY = "a9TIv9g****84UScUZ3Zk30uA"
    CONSUMER_SECRET ="4qcZYvP8RWjK****akMJEPuvu0kZq0vfSc45JOENLpwDiyhFh1"
    ACCESS_TOKEN_KEY = "702455247084453888-****3kaZzXIu1NmNoSFvGNFSx3z5P6Z"
    ACCESS_TOKEN_SECRET = "fldNq1f0oHUqOafR****01uxWGxCLJt253lKPCbrX0acx"
    api = twitter.Api(consumer_key = CONSUMER_KEY,\
                        consumer_secret = CONSUMER_SECRET,\
                        access_token_key = ACCESS_TOKEN_KEY,\
                        access_token_secret = ACCESS_TOKEN_SECRET)
    resultsPages = []
    for i in range(1,15):
        print "fetching page %d" % i
        searchResults = api.GetSearch(searchStr, count = 100, since_id = i)
            #, since="2016-02-21")
        resultsPages.append(searchResults)
        sleep(6)
    return resultsPages

def textParse(bigString):
    urlsRemoved = re.sub('(http[s]?:[/][/]|www.)([a-z]|[A-Z]|[0-9]|[/.]|[-])*',\
        '', bigString)
    listOfTokens = re.split(r'\W*', urlsRemoved)
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]

def mineTweets(tweetArr, minSup=5):
    parsedList = []
    for i in range(14):
        for j in range(100):
            parsedList.append(textParse(tweetArr[i][j].text))
    initSet = createInitSet(parsedList)
    myFPtree, myHeaderTab = createTree(initSet, minSup)
    myFreqList = []
    mineTree(myFPtree, myHeaderTab, minSup, set([]), myFreqList)
    return myFreqList

• 运行结果如下。现在是2月24日，2月22日苹果和FBI之间的争论开始，用Apple作为关键词看一下最近的记录。lotsOfTweets的下标是我随机抽取的，大部分都和FBI有关。得到频繁项集可以发现有许多都是fbi、iphone、cifrado等组成，和最近的热点相近。

>>> lotsOfTweets = fpGrowth.getLotsOfTweets('Apple')
fetching page 1
fetching page 2
....https://t.co/rjhZgCPXbC #Apple'
>>> lotsOfTweets[0][89].text
u'RT @BIUK_Tech: Apple will use a free speech defence in its war \with the FBI $AAPL https://t.co/1rI51zTq8p'
with the FBI $AAPL https://t.co/1rI51zTq8p'
>>> lotsOfTweets[1][89].text
u'Watch Bill Gates talk about the privacy debate between Apple and\ the FBI https://t.co/8mQ5smXOYE'
 the FBI https://t.co/8mQ5smXOYE'
>>> lotsOfTweets[2][14].text
u"'Perang Panas' FBI Vs Apple, Publik AS Terbelah: Mayoritas publik\ yang disurvei mendukung FBI. https://t.co/ZNmPT699b1"
 yang disurvei mendukung FBI. https://t.co/ZNmPT699b1"

>>> listOfTerms = fpGrowth.mineTweets(lotsOfTweets, 20)
>>> len(listOfTerms)
1570
>>> for t in listOfTerms:
...     if len(t) == 3 and 'fbi' in t:
...             print t
set([u'fbi', u'cifrado', u'entender'])
set([u'fbi', u'cifrado', u'iphone'])
set([u'fbi', u'del', u'cifrado'])
set([u'fbi', u'entender', u'con'])
set([u'fbi', u'iphone', u'entender'])

FP-growth算法总结

FP-growth算法是一种用于发现数据集中频繁模式的有效方法，利用Apriori原则执行，支队数据集扫描两遍。数据及存储在FP树结构中，该树构建完成后，通过查找元素项的条件模式基、构建条件FP树来发现频繁项集并递归此过程。

---

参考文献： 《机器学习实战 - 美Peter Harrington》

原创作品，允许转载，转载时无需告知，但请务必以超链接形式标明文章原始出处(https://forec.github.io/2016/02/24/machinelearning12/) 、作者信息（Forec）和本声明。