这篇文章中的C语言代码均为md编辑器中手打,仅作理解用,未经过编译测试。有错误请留言,将及时更正。
摘要
需求
基本的数学知识
- 指对数、级数、模运算,常用换底公式,几何/算术级数公式以及同余的一些相关公式。
- log(a)B = log(c)B/log(c)A (c > 0)
- ∑(0->N) A^i < 1/(1-A) (0 < A < 1)
- ∑(1->N) i^2 = N(N+1)(2N+1) / 6 ≈ N^3 / 3
- ∑(1->N) i^k ≈ N^(k+1) / |k+1| (k != -1)
- Hn(调和数) = ∑(1->N) 1 / i ≈ ln N 误差γ(欧拉常数) ≈ 0.57721566
- A+C≡B+C(mod N) && AD≡BD(mod N) (A≡B mod N)
- 数学归纳法和反证法
- 递归和算法时空复杂度分析(离散数学上册,考虑最坏结果)
- 一个经典的例子:最大子序列和问题,在本文底部。
- 一般估计:根据循环嵌套得到的迭代次数估计复杂度
- 常可寻找的优化:递推式取代循环,分治,循环数组,记忆化。
三种基本数据结构ADT
抽象数据类型(abstract data type, ADT)是一些操作的集合:例如对于集合ADT,可以有如交、并、测定长度等操作,也可以只有交、并两种操作,这从集合上定义了两种不同的ADT。
表ADT
- 对表(list)的所有操作可以通过数组实现
- 需要估计表所需数组的最大长度,资源浪费
- PrintList和FindItem以线性时间执行,且FindKth为常数时间
- Insert和Delete操作最坏时间复杂度为O(N),平均情况下每次操作均需移动表中一般的元素
- 链表
- 减少Insert和Delete操作的线性开销(根本在于表的存储不是连续的)
- FindKth以线性时间执行
- 数组模拟链表,类似图的前向星表示法,采用一组cursor实现(游标)。
- 两个实例单向链表的类型声明及其ADT包含的操作和链表实现基数排序在本文底部。
栈ADT
- 栈(stack)是的插入和删除操作只能在一个位置上进行的表,该位置为表的末端,称为栈顶(top)。
- 应用
- 平衡符号
- 逆波兰表达式,在本文底部有其实现方式的简单介绍。
- 函数调用的存储工作由系统栈完成,尽量避免尾递归。
队列ADT
- 基本操作是入队(Enqueue)和出队(Dequeue),先进先出。
- 需要注意队列是否为空的条件。循环队列可以满足一些问题的模型,同时改善数组实现队列的空间利用率。
- 应用
- 约瑟夫环问题,链表模拟实现代码在本文例程中。
- 排队作业问题
- 队列ADT数组模拟代码实现
树
树的实现、遍历和应用
- 基本概念
每个节点可以有任意多个子女,也可能没有子女。没有子女的节点为叶子结点(树叶),具有相同父亲的节点为兄弟。 实现
每个节点包含一个指向其第一个子女的指针(向下),和一个指向其下一个兄弟的指针(平行)。1
2
3
4
5struct TreeNode{
ElementType element;
struct TreeNode * firstChild;
struct TreeNode * nextBrother;
}遍历和应用
- 应用:操作系统的目录结构
- 遍历方式:先序遍历(先处理父亲节点,如打印目录内全部文件),后序遍历(先处理诸子女,如统计该目录所占空间大小)
二叉树
二叉树的每个节点不能有多于两个子女
平均二叉树的深度为O(sqrt(N)),二叉查找树的平均深度为O(logN),可达最坏深度为N-1。
二叉树的数学基础
- 高度为h的二叉树至多有2^h 个叶子结点;高度为h≥0的二叉树至少有h+1个结点;高度不超过h(≥0)的二叉树至多有2^h+1 -1个结点;含有n≥1个结点的二叉树的高度至多为n-1;含有n≥1个结点的二叉树的高度至少为logn,因此其高度为Ω(logn)。
- 满二叉树:高度为h的满二叉树,共有2^h+1 -1个结点;共有2^h 个叶子,共有2^h -1个内结点,内结点个数比叶子少1。
- 完全二叉树:第h层的从左到右第k个结点的编号为2^h +k-1;叶子个数或者和内结点个数相等或者多1;通过本结点的编号可以快速得到父结点(i/2)、左右孩子(2×i,2×i+1)的编号。
表达式树
- 表达式树的操作数是树叶,其他节点为操作符。方便起见,假设所有操作均为二元的,则该表达式树刚好是二叉树(节点有可能含有多于两个子女,或只含有一个子女,如单目运算符)。
此时分别先序(中左右),中序(左中右),后序(左右中)遍历,得到的即为对应的前缀,中缀和后缀表达式。 - 由后缀表达式构造表达式树:类似后缀表达式求值,若遇到操作数直接压栈,遇到操作符则弹出栈顶的两棵树T1,T2作为操作符的两个子女,构成一棵新的树,此树的根为操作符,并将其指针压入栈中。
- 表达式树的操作数是树叶,其他节点为操作符。方便起见,假设所有操作均为二元的,则该表达式树刚好是二叉树(节点有可能含有多于两个子女,或只含有一个子女,如单目运算符)。
二叉查找树
以整型数据为例,假设不存在重复的关键字(重复情况可以增加一个count域记录)
- 对于树中每个节点X,其左子树中所有关键字均小于X,右子树中所有关键字均大于X
- 类型声明
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15struct TreeNode{
int value;
struct TreeNode * left;
struct TreeNode * right;
};
#ifndef _Tree_
typedef struct TreeNode * node;
void MakeEmpty( node root );
node Find( int x, node root );
node Findmin( node root );
node Findmax( node root );
node Insert( int x, node root );
node Delete( int x, node root );
#endif
操作实现
Find(注意测试空树)
1
2
3
4
5
6
7
8
9
10node Find( int x, node root ){
if ( root == NULL )
return NULL;
if ( x == root->value )
return root;
if ( x < root->value )
return Find( x, root->left );
else
return Find( x, root->right );
} /*这里的尾递归可以用迭代代替,但其使用的栈空间只有O(logN)*/递归版本的Findmin和迭代版本的Findmax
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15node Findmin( node root ){
if ( root == NULL )
return NULL;
else if ( root->left == NULL )
return root;
else
return Findmin( root->left );
}
node Findmax( node root ){
if ( root != NULL )
node temp = root;
while ( temp->right != NULL )
temp = temp->right;
return temp;
}Insert
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17node Insert( int x, node root ){
if ( root == NULL ){
root = malloc( sizeof ( struct TreeNode ) );
if ( root == NULL )
FatalError("flood");
else{
root->value = x;
root->left = root->right = NULL;
}
}
else if ( x < root->value )
root->left = Insert( x, root->left );
else if ( x > root->value )
root->right = Insert( x, root->right );
/* count++ if x == root->value */
return root;
}Delete,若要删除的节点没有子女则直接删除,有一个子女则使用其子女将其替代,若有两个子女,则寻找其后继节点(其右子树中最左节点),使用该后继节点(此节点一定最多只有一个子女)代替要删除的节点,并删除该后继节点。当删除次数不多时,可以采用懒惰删除,被删除的节点仍留在树中,但做一个删除的标记。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23node Delete( int x, node root ){
if ( root == NULL )
Error("Empty tree");
else if ( x < root->value )
root->left = Delete( x, root->left );
else if ( x > root->value )
root->right = Delete( x, root->right );
else /* Found */
if ( root->left != NULL && root->right != NULL ){
node temp = Findmin( root->right );
root->value = temp->value;
root->right = Delete( root->value, root->right );
}
else {
node temp = root;
if ( root->left == NULL )
root = root->right;
else
root = root->left;
free( temp );
}
return root;
}
平均分析
当二叉查找树不够平衡时,或者退化成一条直线时,所有操作都会成为线性开销。常用的解决办法是为二叉查找树附加一个平衡结构条件,使得任何节点的深度都不能过深。这种做法非常麻烦,并且更新树结构需要很长时间,但防止了查找树的退化。例如最老的一种平衡查找树(AVL树),红黑树,treap等。比较新的做法是splay tree(伸展树或分裂树),放弃平衡条件,允许树有任意深度,但每次操作后要对树结构调整,使后面的操作效率提高。此时对于任意单个运算无法保证O(logN)的时间复杂度,但可证明连续M次操作在最坏情形下的花费时间为O(MlogN)。
AVL树
一棵AVL树的每个节点的左子树和右子树的高度最多差1。
AVL树的平衡维护
AVL树平衡条件破坏的可能情况
- 在插入一个新节点之后,只有从插入点到根结点的路径上的节点可能不平衡,因为只有这些节点的子树可能发生变化。沿着这条路径上行到根并更新平衡信息,就可以找到某个平衡性被破坏的节点。假设这个平衡性被破坏的节点是X,因为任意节点最多能有两个孩子,所以高度不平衡的情况下,X的两棵子树高度差2。这种不平衡可能源于下面四种情况:
- 对X的左孩子的左子树进行了一次插入
- 对X的左孩子的右子树进行了一次插入
- 对X的右孩子的左子树进行了一次插入
- 对X的右孩子的右子树进行了一次插入
- 上面四种情况中,第一种和第四种是关于X的镜面对称,第二种和第三种是关于X的镜面对称。因此只需要考虑前两种情况,并拓展到后两种情况。下面对前两种情况分别分析,这两种情况的处理方法在其他平衡树中也多有使用。
对X左孩子的左子树插入。此时为(左-左)或(右-右)情况,发生在树的“外边”,可以通过一次单旋转完成调整。以下图片来源于网络。
下面的两张图分别是调整第一种和第四种情况的单旋转。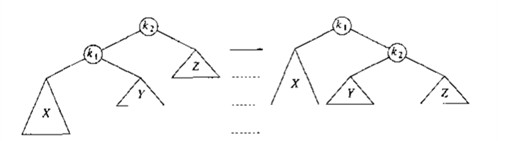
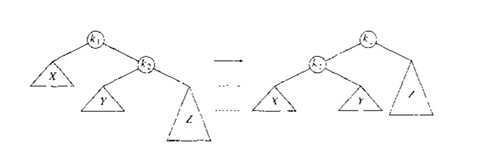
下面的两张图分别是两种情况的实例,上面的图是第一种情况(右旋转),下面的图为第四种情况(左旋转)。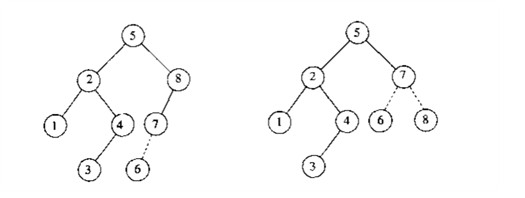
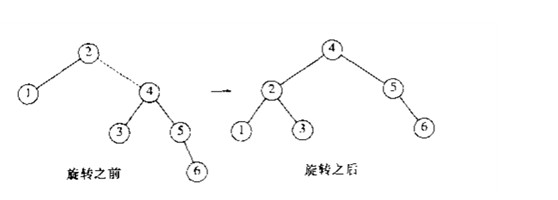
需要注意的是,当旋转修正树的部分结构时,树的其余部分必须知晓这部分变化。比如实例的第一张图中,6,7,8旋转后,5的右孩子必须指向7,来代替原来的8。- 对X左孩子的右子树插入。此时为(左-右)或(右-左)情况,发生在树的“内侧”,可以通过双旋转修正。
如下图所示是一个双旋转过程(图片来源于Vamei)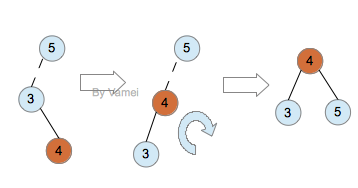
下面两张图分别是LR旋转(针对左孩子的右子树插入)和RL旋转(针对右孩子的左子树插入)。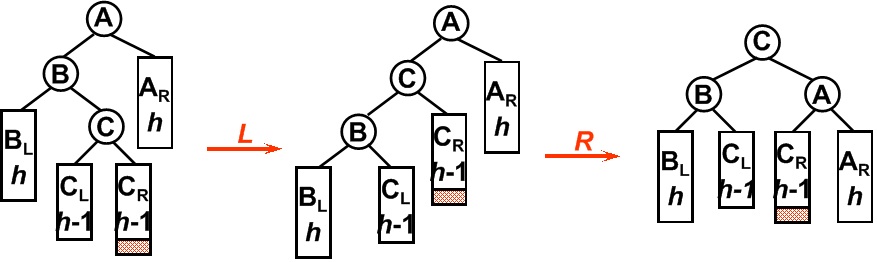
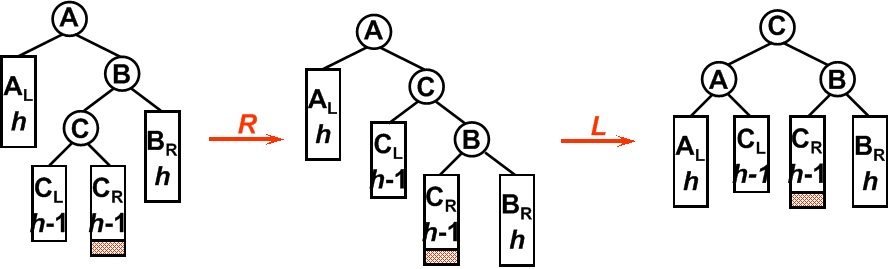
以LR旋转为例,B节点处不满足AVL树性质,对B-C支作左旋转,使得C成为C-B支新的根,之后A-C支右旋转,使得C成为整棵树的新根,满足AVL树性质。
AVL树的代码实现
节点声明
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21#ifndef _AvlTree_H
struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;
typedef int ElementType; /* ElementType */
AvlTree MakeEmpty( AvlTree T );
AvlTree Insert( ElementType x, AvlTree T );
AvlTree Delete( ElementType x, AvlTree T );
Position Find( ElementType x, AvlTree T );
Position Findmin( AvlTree T );
Position Findmax( AvlTree T );
void Destroy( AvlTree T );
#endif /* _AvlTree_H */
struct AvlNode{
ElementType element;
AvlTree left;
AvlTree right;
int height;
};功能实现(Find,Findmin和Findmax操作与二叉查找树完全相同)
获取节点高度
1
2
3
4
5
6static int Height( Position P ){
if ( P == NULL )
return -1;
else
return P->height;
}右旋转(针对第一种情况)和左旋转(针对第四种情况)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16static Position SingleRightRotate( Position K2 ){
Position K1 = K2->left;
K2->left = K1->right;
K1->right = K2;
K2->height = Max( Height( K2->left ), Height( K2->right ) ) + 1;
K1->height = Max( Height( K1->left ), K2->height ) + 1;
return K1; /* K1 is the new root */
}
static Position SingleLeftRotate( Position K1 ){
Position K2 = K1->right;
K1->right = K2->left;
K2->left = K1;
K1->height = Max( Height( K1->right ), Height( K1->left ) ) + 1;
K2->height = Max( K1->height, Height( K2->right ) ) + 1;
return K2; /* K2 is the new root */
}LR旋转(针对第二种情况)和RL旋转(针对第三种情况)
1
2
3
4
5
6
7
8static Position DoubleLeftRightRotate( Position K3 ){
K3->left = SingleLeftRotate( K3->left );
return SingleRightRotate( K3 );
}
static Position DoubleRightLeftRotate( Position K3 ){
K3->right = SinglerightRotate( K3->right );
return SingleLeftRotate( K3 );
}插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31AvlTree Insert( ElementType x, AvlTree T ){
if ( T == NULL ){
/* Empty Tree, Create a one-node tree */
T = ( AvlTree )malloc( sizeof( struct AvlNode ) );
if ( T == NULL )
FatalError( "flood" );
else {
T->element = x;
T->height = 0;
T->left = T->right = NULL;
}
}
else if ( x < T->element ){
T->left = Insert( x, T->left );
if ( Height( T->left ) - Height( T->right ) == 2 )
if ( x < T->left->element )
T = SingleRightRotate( T );
else
T = DoubleLeftRight( T );
}
else if ( x > T->element ){
T->right = Insert( x, T->right );
if ( Height( T->right ) - Height( T->left ) == 2 )
if ( x > T->right->element )
T = SingleLeftRotate( T );
else
T = DoubleRightLeftRotate( T );
}
T->height = Max( Height( T->left ), Height( T->right ) ) + 1;
return T;
}删除(AVL树删除操作相对比较复杂,删除操作较少时可以懒惰删除减少代码编写量)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42static AvlTree Delete( ElementType x, AvlTree T ){
if ( T == NULL )
Error("Empty Tree");
else if ( x < T->element ){
T->left = Delete( x, T->left );
if ( Height( T->right ) - Height( T->left ) == 2){
if ( T->right != NULL ){
if ( Height( T->right->left ) > Height( T->right->right ) )
T = DoubleRightLeftRotate( T );
else
T = SingleLeftRotate( T );
}
}
}
else if ( x > T->element ){
T->right = Delete( x, T->right );
if ( Height( T->left ) - Height( T->right ) == 2){
if ( T->left != NULL ){
if ( Height( T->left->right ) > Height( T->left->left ) )
T = DoubleLeftRotate( T );
else
T = SingleRightRotate( T );
}
}
}
else /* Found */
if ( T->left != NULL && T->right != NULL ){
Position temp = Findmin( T->right );
T->value = temp->value;
T->right = Delete( T->value, T->right );
}
else {
Position temp = T;
if ( T->left == NULL )
T = T->right;
else
T = T->left;
free( temp );
}
if ( T != NULL )
T->height = Max( Height( T->left ), Height( T->right ) ) + 1;
return T;销毁
1
2
3
4
5
6
7
8static void Destroy( AvlTree T ){
if ( T == NULL )
return;
Destroy( T->left );
Destroy( T->right );
free( T );
T = NULL;
}
红黑树
红黑树也是一种二叉查找树,但在其每个节点上增加一个存储位表示节点的颜色(红或黑)。通过对节点着色的限制,可以使得红黑树没有任何一条路径可能比其他路径长两倍,因此整棵红黑树接近平衡。
采用一个哨兵NIL(外节点)来代替空指针,NIL是和红黑树内普通节点有相同域的对象,其color域为BLACK,其他域可以设置为任意值。所有指向NULL的指针都将指向NIL。
红黑性质
- 每个节点或是红的或是黑的
- 根节点是黑的,每个叶节点(NIL)也是黑的
- 如果一个节点是红的,则它的两个子女都是黑的
- 对每个节点,从该节点到其子孙节点的所有路径上包含相同数目的黑色节点
- 一棵有n个内节点的红黑树,其高度至多为2lg(n+1),证明使用数学归纳法。
- 旋转操作:insert和delete都可能使新的红黑树违反红黑性质。下图展示了左旋和右旋两种状态的切换

红黑树的代码实现
类型声明
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24#ifndef _RBT_H
typedef struct RbNode * Position;
typedef struct RbNode * RbTree;
void LeftRotate( RbTree T, Position x );
void RightRotate( RbTree T, Position x );
void Insert( RbTree T, Position x );
void Delete( RbTree T, Position x );
void InsertFixup( RbTree T, Position x );
void DeleteFixup( RbTree T, Position x );
#endif
enum COLOR = { RED , BLACK };
struct RbNode{
ElementType value;
struct RbNode * left;
struct RbNode * right;
struct RbNode * parent;
enum COLOR color;
};
struct RbNode * NIL = ( RbNode * ) malloc ( sizeof ( struct RbNode ) );
struct RbNode * root = NIL;
NIL->color = BLACK;旋转操作
左旋
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void LeftRotate( RbTree T, Position x ){
if ( x == NIL || x->right == NIL )
return;
Position y = x->right;
y->parent = x->parent;
x->right = y->left;
if ( y->left != NIL )
y->left->parent = x;
if ( x->parent == NIL ){
root = y;
NIL->left = root;
NIL->right = root;
}
else {
if ( x == x->parent->left )
x->parent->left = y;
else x->parent->right = y;
}
y->left = x;
x->parent = y;
}右旋(和左旋相对应)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22void RightRotate( RbTree T, Position y ){
if ( y == NIL || y->left == NIL )
return;
Position x = y->left;
x->parent = y->parent;
y->left = x->right;
if ( x->right != NIL )
x->right->parent = y;
if ( y->parent == NIL ){
root = x;
NIL->left = root;
NIL->right = root;
}
else {
if ( y == y->parent->right )
y->parent->right = x;
else
y->parent->left = x;
}
x->right = y;
y->parent = x;
}
插入操作
- 红黑树的插入操作时,新插入的节点默认颜色红色,因此可能破坏红黑性质共有三种情况:1.当前插入节点的父节点和叔叔节点都是红色,2.当前插入节点的父亲节点是红色,叔叔节点是黑色,插入节点是父亲节点的右孩子,3.在2中的情况,插入节点是父亲节点的左孩子。
插入代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void Insert( RbTree T, Position z ){ // z has already been allocated storage
Position y = NIL;
Position x = root;
while ( x != NIL ){
y = x;
if ( z->value < x->value )
x = x->left;
else
x = x->right;
}
z->parent = y;
if ( y == NIL )
root = z;
else if ( z->value < y->value )
y->left = z;
else
y->right = z;
z->left = z->right = NIL;
z->color = RED;
InsertFixup( T, z );
}插入修复代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41void InsertFixup( RbTree T, Position z ){
while ( z->parent->color == RED ){
if ( z->parent == z->parent->parent->left ){
Position y = z->parent->parent->right;
if ( y->color == RED ){ // case 1
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else {
if ( z == z->parent->right ){ // case 2
z = z->parent;
LeftRotate( T, z );
}
z->parent->color = BLACK; // case 3
z->parent->parent->color = RED;
RightRotate( T, z->parent->parent );
}
}
else if ( z->parent == z->parent->parent->right ){
Position y = z->parent->parent->left;
if ( y->color == RED ){
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else {
if ( z == z->parent->left ){
z = z->parent;
RightRotate( T, z );
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
LeftRotate( T, z->parent->parent );
}
}
}
root->color = BLACK;
}
删除操作
- 删除操作:如果被删除节点是黑色(假设它是其父节点的左孩子),可能有四种情况破坏红黑性质:1.被删除节点的兄弟节点是红色(此时父节点和兄弟节点的子节点都是黑色),2.兄弟节点是黑色且兄弟节点的两个子节点都是黑色,3.兄弟节点是黑色,兄弟节点的左孩子是红色,右孩子是黑色,4.兄弟节点是黑色,兄弟节点的右孩子是红色,左孩子颜色随意。
删除代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27void Delete( RbTree T, Position z ){ // z has already been found
Position x, y;
if ( z->left == NIL || z->right == NIL )
y = z;
else
y = Findmin( z->right );
if ( y->left != NIL )
x = y->left;
else x = y->right;
x->parent = y->parent;
if ( y->parent == NIL ){
root = x;
NIL->left = root;
NIL->right = root;
}
else{
if ( y == y->parent->left )
x = y->parent->left;
else
x = y->parent->right;
}
if ( y != z )
z->value = y->value;
if ( y->color == BLACK )
DeleteFixup( T, x );
free(y);
}删除恢复红黑性质代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57void DeleteFixup( RbTree T, Position x ){
Position w;
while ( x != root && x->color == BLACK ){
if ( x == x->parent->left ){
w = x->parent->right;
if ( w->color == RED ){ // case 1
w->color = BLACK;
x->parent->color = RED;
LeftRotate( T, x->parent );
w = x->parent->right;
}
else if ( w->left->color == BLACK && w->right->color == BLACK ){ // case 2
w->color = RED;
x = x->parent;
}
else {
if ( w->right->color == BLACK ){ // case 3
w->left->color = BLACK;
w->color = RED;
RightRotate( T, w );
w = x->parent->right;
} // case 4
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
LeftRotate( T, x->parent );
x = root;
}
}
else if ( x == x->parent->right ){
w = x->parent->left;
if ( w->color == RED ){
w->color = BLACK;
x->parent->color = RED;
RightRotate( T, x->parent );
w = x->parent->left;
}
if ( w->left->color == BLACK && w->right->color == BLACK ){
w->color = RED;
x = x->parent;
}
else {
if ( w->left->color == BLACK ){
w->right->color = BLACK;
w->color = RED;
LeftRotate( T, w );
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
RightRotate( T, x->parent );
x = root;
}
}
x->color = BLACK;
}
原创作品,允许转载,转载时无需告知,但请务必以超链接形式标明文章原始出处(https://forec.github.io/2015/09/08/Data-Structure-basis1/) 、作者信息(Forec)和本声明。